题目内容
已知：如图，AD是⊙O的直径，BC是⊙O的弦，AD⊥BC，垂足为点E，BC=8，AD=10．
求：（1）OE的长；
（2）∠B的正弦值．
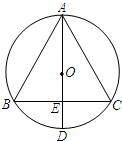
求：（1）OE的长；
（2）∠B的正弦值．
（1）连接OE，OB，如图所示：
∵直径AD=10，
∴AO=OB=OD=5，
又AD⊥BC，
∴E为BC的中点，又BC=8，
∴BE=CE=
BC=4，
在Rt△BOE中，OB=5，BE=4，
根据勾股定理得：OE=
=3；
（2）∵AO=5，OE=3，
∴AE=AO+OE=5+3=8，
在Rt△ABE中，BE=4，AE=8，
根据勾股定理得：AB=
=4
，
则sin∠ABC=
=
=
．
∵直径AD=10，
∴AO=OB=OD=5，
又AD⊥BC，
∴E为BC的中点，又BC=8，
∴BE=CE=
| 1 |
| 2 |
在Rt△BOE中，OB=5，BE=4，
根据勾股定理得：OE=
| OB2-BE2 |
（2）∵AO=5，OE=3，
∴AE=AO+OE=5+3=8，
在Rt△ABE中，BE=4，AE=8，
根据勾股定理得：AB=
| AE2+BE2 |
| 5 |
则sin∠ABC=
| AE |
| AB |
| 8 | ||
4
|
2
| ||
| 5 |
练习册系列答案
开心蛙口算题卡系列答案
相关题目
