题目内容
19.已知:α=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$,b=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$,求a2-5ab+b2的值.分析 首先利用分母有理化化简a、b,然后再把a2-5ab+b2化成(a-b)2-3ab,然后代入求值即可.
解答 解:α=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$=$\frac{(\sqrt{3}-\sqrt{2})^{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=5-2$\sqrt{6}$,
b=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$=$\frac{(\sqrt{3}+\sqrt{2})^{2}}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}$=5+2$\sqrt{6}$,
a2-5ab+b2=(a-b)2-3ab=(-4$\sqrt{6}$)2-3×(5-2$\sqrt{6}$)(5+2$\sqrt{6}$)=96-3×(25-24)=93.
点评 此题主要考查了二次根式的化简求值,关键是掌握分母有理化的方法.

练习册系列答案
相关题目
7.在实数中,立方根等于它本身的数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数个 |
 用一根长为l的铁丝,制成如图所示的框架,问:宽x是多少时,框架的面积最大?最大面积是多少?
用一根长为l的铁丝,制成如图所示的框架,问:宽x是多少时,框架的面积最大?最大面积是多少?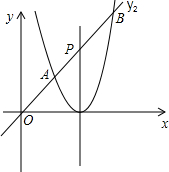 将抛物线y1=2x2向右平移2个单位长度,得到抛物线y2的图象,如图所示.
将抛物线y1=2x2向右平移2个单位长度,得到抛物线y2的图象,如图所示.