题目内容
3.张浩有红牌和蓝牌各75张,已知张浩能在一个摊位上用2张红牌换1张银牌和1张蓝牌,还能在另一个摊位上用3张蓝牌换1张银牌和1张红牌,若他按照上述方法继续换下去,直到手中的牌无法交换为止,则张浩手中最后有银牌( )张.| A. | 62 | B. | 82 | C. | 102 | D. | 103 |
分析 利用2张红牌换1张银牌和1张蓝牌,3张蓝牌换1张银牌和1张红牌,分别结合牌的张数表示出每次换取的银牌张数以及对应红或蓝牌的数量进而求出答案.
解答 解:由题意可得:用75张红牌可以换37张银牌和37张蓝牌,
此时还剩1张红牌,还剩75+37=112(张)蓝牌,
则利用112张蓝牌可以换37张银牌和37张红牌,
此时还剩1张蓝牌,还剩1+37=38(张)红牌,
则利用38张红牌可以换19张银牌和19张蓝牌,
此时还剩20张蓝牌,
则利用20张蓝牌可以换6张银牌和6张红牌,
此时还剩2张蓝牌,还剩6张红牌,
则利用6张红牌可以换3张银牌和3张蓝牌,
此时,还剩5张蓝牌,
则利用5张蓝牌可以换1张银牌和1张红牌,
此时还剩2张蓝牌,还剩1张红牌,到此结束.
故张浩手中最后有银牌:37+37+19+6+3+1=103(张).
故选:D.
点评 此题主要考查了推理与论证,根据已知利用列举法分别表示出每次换取后的牌的张数是解题关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
11.方程y2=-a有实数根的条件是( )
| A. | a≤0 | B. | a≥0 | C. | a>0 | D. | a为任何实数 |
15.鸡兔同笼,上数有20个头,下数有50条腿,可知鸡兔和数量分别为( )
| A. | 5和15 | B. | 15和5 | C. | 12和8 | D. | 8和12 |
 如图,若∠C=30°,求∠A+∠B+∠D+∠E的度数.
如图,若∠C=30°,求∠A+∠B+∠D+∠E的度数. 如图,5个全等的正六边形,A、B、C、D、E,请仔细观察A、B、C、D四个答案,其中与右方图案完全相同的是( )
如图,5个全等的正六边形,A、B、C、D、E,请仔细观察A、B、C、D四个答案,其中与右方图案完全相同的是( )



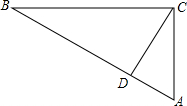 已知:如图,在△ABC中,∠A=60°,CD⊥AB,BC=2CD,AD=$\sqrt{3}$,求AB的长.
已知:如图,在△ABC中,∠A=60°,CD⊥AB,BC=2CD,AD=$\sqrt{3}$,求AB的长.