题目内容
如图，∠AOB=130°，射线OC是么AOB内部任意一条射线，OD、OE分别是么AOC、∠BOC的平分线，下列叙述正确的是
- A.∠DOE的度数不能确定
- B.∠AOD=
EOC - C.∠BOE=2∠COD
- D.∠AOD+∠BOE=65°
D
分析：本题是对角的平分线的性质的考查，角平分线将角分成相等的两部分．结合选项得出正确结论．
解答：∵OD、OE分别是∠AOC、∠BOC的平分线，
∴∠AOD=∠COD、∠EOC=∠BOE，
又∵∠AOD+∠BOE+∠EOC+∠COD=∠AOB=130°，
∴∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°．
故选D．
点评：本题是对角平分线的性质的考查．然后根据角平分线定义得出所求角与已知角的关系转化求解．
分析：本题是对角的平分线的性质的考查，角平分线将角分成相等的两部分．结合选项得出正确结论．
解答：∵OD、OE分别是∠AOC、∠BOC的平分线，
∴∠AOD=∠COD、∠EOC=∠BOE，
又∵∠AOD+∠BOE+∠EOC+∠COD=∠AOB=130°，
∴∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°．
故选D．
点评：本题是对角平分线的性质的考查．然后根据角平分线定义得出所求角与已知角的关系转化求解．
练习册系列答案
名校课堂系列答案
相关题目
（2013•石景山区二模）如图，∠AOB=45°，过OA上到点O的距离分别为1，4，7，10，13，16，…的点作OA的垂线与OB相交，得到并标出一组黑色梯形，它们的面积分别为s1，s2，s3，…，观察图中的规律，第4个黑色梯形的面积S4=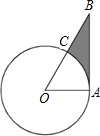
（2012•三明）如图，AB是⊙O的切线，切点为A，OA=1，∠AOB=60°，则图中阴影部分的面积是（ ）
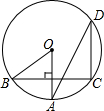（2013•门头沟区一模）如图，OA是⊙O的半径，弦BC⊥OA，D是⊙O上一点，若∠ADC=26°，则∠AOB的度数为（ ）
如图，∠AOB=60°，且∠AOC=
如图，∠AOB=45°，过OA上到点O的距离分别为1，4，7，10，13，16，…的点作OA的垂线与OB相交，得到并标出一组黑色梯形，它们的面积分别为s1，s2，s3，…，观察图中的规律，第4个黑色梯形的面积S4=________，第n（n为正整数）个黑色梯形的面积Sn=________．