题目内容
 (2013•石景山区二模)如图,∠AOB=45°,过OA上到点O的距离分别为1,4,7,10,13,16,…的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为s1,s2,s3,…,观察图中的规律,第4个黑色梯形的面积S4=
(2013•石景山区二模)如图,∠AOB=45°,过OA上到点O的距离分别为1,4,7,10,13,16,…的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为s1,s2,s3,…,观察图中的规律,第4个黑色梯形的面积S4=| 123 |
| 2 |
| 123 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
分析:根据题意可得每一个小梯形的上下底长,根据梯形的面积公式可以计算出每一个小梯形的面积,再根据结果找出规律即可.
解答:解:由题意得:s1=(1+4)×3÷2=
×5=
,
s2=(7+10)×3÷2=
×17=
,
s3=(13+16)×3÷2=
×29=
,
s4=(19+22)×3÷2=
×41=
;
…
sn=
(12n-7).
故答案为:
;
(12n-7).
| 3 |
| 2 |
| 15 |
| 2 |
s2=(7+10)×3÷2=
| 3 |
| 2 |
| 51 |
| 2 |
s3=(13+16)×3÷2=
| 3 |
| 2 |
| 81 |
| 2 |
s4=(19+22)×3÷2=
| 3 |
| 2 |
| 123 |
| 2 |
…
sn=
| 3 |
| 2 |
故答案为:
| 123 |
| 2 |
| 3 |
| 2 |
点评:此题主要考查了直角梯形,关键是掌握梯形的面积公式=(上底+下底)×高÷2.

练习册系列答案
相关题目
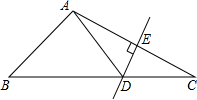 (2013•石景山区二模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
(2013•石景山区二模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( ) (2013•石景山区二模)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )
(2013•石景山区二模)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )