题目内容
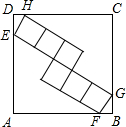 如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则每个小正方形的边长为
如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则每个小正方形的边长为考点:勾股定理,全等三角形的判定与性质,正方形的性质
专题:
分析:如图,过点G作GP⊥AD,垂足为P,可以得到△BGF∽△PGE,再根据相似三角形对应边成比例的性质列式求解即可得到DE和BG,根据勾股定理可求EG的长,进而求出每个小正方形的边长.
解答:解:如图所示:
∵正方形ABCD边长为25,
∴∠A=∠B=90°,AB=25,
过点G作GP⊥AD,垂足为P,则∠4=∠5=90°,
∴四边形APGB是矩形,
∴∠2+∠3=90°,PG=AB=25,
∵六个大小完全一样的小正方形如图放置在大正方形中,
∴∠1+∠2=90°,
∴∠1=∠FGB,
∴△BGF∽△PGE,
∴
=
,
∴
=
,
∴GB=5.
∴AP=5.
同理DE=5.
∴PE=AD-AP-DE=15,
∴EG=
=5
,
∴小正方形的边长为
.
故答案为:
.
∵正方形ABCD边长为25,
∴∠A=∠B=90°,AB=25,
过点G作GP⊥AD,垂足为P,则∠4=∠5=90°,
∴四边形APGB是矩形,

∴∠2+∠3=90°,PG=AB=25,
∵六个大小完全一样的小正方形如图放置在大正方形中,
∴∠1+∠2=90°,
∴∠1=∠FGB,
∴△BGF∽△PGE,
∴
| BG |
| PG |
| FG |
| EG |
∴
| BG |
| 25 |
| 1 |
| 5 |
∴GB=5.
∴AP=5.
同理DE=5.
∴PE=AD-AP-DE=15,
∴EG=
| 152+252 |
| 34 |
∴小正方形的边长为
| 34 |
故答案为:
| 34 |
点评:本题主要考查了利用相似三角形的判定和相似三角形对应边成比例的性质和勾股定理,综合性较强,正确的作出辅助线是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
下列计算中正确的是( )
| A、(-14)-(+5)=-9 |
| B、0-(-5)=5 |
| C、-3-3=0 |
| D、-5-2=-3 |
下列说法正确的是( )
| A、负数没有倒数 |
| B、正数的倒数比自身小 |
| C、任何有理数都有倒数 |
| D、倒数等于本身的数是-1或1 |
下列选项中无理数是( )
| A、3.14159 | |||
B、
| |||
| C、π | |||
D、4.
|
在钻石联赛上海站男子跳远比赛中,澳大利亚名将瓦特以8.44米的成绩夺得冠军,裁判测量跳远成绩依据的数学知识是( )
| A、两点之间,线段最短 |
| B、两点确定一条直线 |
| C、点到直线的距离 |
| D、垂直的定义 |
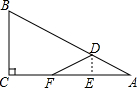 如图,在△ABC中,∠C=90°,∠A=30°,BC=3,点D、E分别在AB、AC上,将△ABC沿DE折叠,点A落在AC边的点F处.若F为CE的中点,则DF的长为( )
如图,在△ABC中,∠C=90°,∠A=30°,BC=3,点D、E分别在AB、AC上,将△ABC沿DE折叠,点A落在AC边的点F处.若F为CE的中点,则DF的长为( )