题目内容
 如图,已知AD⊥CD于D,且AD=4,CD=3,AB=12,BC=13.求四边形ABCD的面积.
如图,已知AD⊥CD于D,且AD=4,CD=3,AB=12,BC=13.求四边形ABCD的面积.考点:勾股定理
专题:
分析:连接AC,先根据勾股定理求出AC的长,再由勾股定理的逆定理判断出△ABC的形状,根据S四边形ABCD=S△ABC+S△ACD即可得出结论.
解答: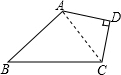 解:连接AC,
解:连接AC,
∵AD⊥CD,AD=4,CD=3,
∴AC=
=
=5.
在△ABC中,
∵AB=12,BC=13,AC=5,52+122=132,即AC2+AB2=BC2,
∴△ABC是直角三角形.
∴S四边形ABCD=S△ABC+S△ACD
=
AD•CD+
AB•AC
=
×3×4+
×12×5
=6+30
=36.
 解:连接AC,
解:连接AC,∵AD⊥CD,AD=4,CD=3,
∴AC=
| AD2+CD2 |
| 42+32 |
在△ABC中,
∵AB=12,BC=13,AC=5,52+122=132,即AC2+AB2=BC2,
∴△ABC是直角三角形.
∴S四边形ABCD=S△ABC+S△ACD
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=6+30
=36.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各组数中,数值相等的是( )
| A、32和23 |
| B、(-2)3和-23 |
| C、-32和(-3)2 |
| D、-(-2)和-|-2| |
下列计算中正确的是( )
| A、(-14)-(+5)=-9 |
| B、0-(-5)=5 |
| C、-3-3=0 |
| D、-5-2=-3 |
下列说法正确的是( )
| A、负数没有倒数 |
| B、正数的倒数比自身小 |
| C、任何有理数都有倒数 |
| D、倒数等于本身的数是-1或1 |
下列选项中无理数是( )
| A、3.14159 | |||
B、
| |||
| C、π | |||
D、4.
|
 如图,点A、B、C在⊙O上,OD⊥AB于点D,OE⊥CB于点E,弧AB度数为40°,弧CB的度数为50°,且DE=6,则⊙O半径的长度是
如图,点A、B、C在⊙O上,OD⊥AB于点D,OE⊥CB于点E,弧AB度数为40°,弧CB的度数为50°,且DE=6,则⊙O半径的长度是