题目内容
13．解方程组：$\left\{\begin{array}{l}{xy+x=3}\\{3xy+y=8}\end{array}\right.$．分析 由方程①可知y=$\frac{3-x}{x}$，代入方程②可得一个关于x的一元二次方程，进行解答，求出x值，再进一步求y即可．
解答 解：$\left\{\begin{array}{l}{xy+x=3①}\\{3xy+y=8②}\end{array}\right.$，
由①得y=$\frac{3-x}{x}$③，
把y=$\frac{3-x}{x}$代入②得：3x×$\frac{3-x}{x}$+$\frac{3-x}{x}$=8，
解得：x1=1，x2=-1；
把x1=1，x2=-1代入③得y1=2，y2=-4，
故方程组的解为$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=2}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=-4}\end{array}\right.$．
点评 考查了高次方程，碰到一时难以下手的问题时，应从最简单的方程入手来找突破口．
练习册系列答案
名校课堂系列答案
相关题目
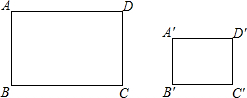如图所示，有矩形ABCD和矩形A′B′C′D′，AB=8cm，BC=12cm，A′B′=4cm，B′C′=6cm．