题目内容
6.已知抛物线y=-$\sqrt{3}$x2+bx+c与x轴交于点A(1,0),B(3,0),与y轴交于点C,抛物线的顶点为D.(1)求b,c的值及顶点D的坐标;
(2)如图1,点E是线段BC上的一点,且BC=3BE,点F(0,m)是y轴正半轴上一点,连接BF,EF与线段OB交于点G,OF:OG=2:$\sqrt{3}$,求△FEB的面积;
(3)如图2,P为线段BC上一动点,连接DP,将△DBP绕点D顺时针旋转60°得△DB′P′(点B的对应点是点B′,点P的对应点是点P′),DP′交y轴于点M,N为MP′的中点,连接PP′,NO,延长NO交BC于点Q,连接QP,若△PP′Q的面积是△BOC面积的$\frac{1}{9}$,求线段BP的长.

分析 (1)把A和B代入函数解析式,解方程组求得b和c的值,进而利用配方法求得顶点坐标;
(2)首先证明△DFG∽△HFE,根据相似三角形的性质求得OH、OF和OG的长,根据S△FEB=S△FGB+S△GEB即可求解;
(3)易证△ADB是等边三角形,则B旋转到A的位置,B′P′在x轴上,利用待定系数法求得M的坐标,利用待定系数法求得DP′所在直线的解析式,则M的坐标即可求得,然后求得ND所在直线的解析式,作QQ′⊥x轴,则△Q′BQ为有一个角是60°的直角三角形,根据三角形的面积公式即可列方程求解.
解答 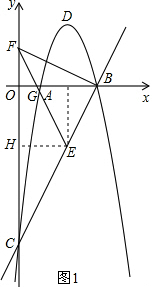 解:(1)根据题意得:$\left\{\begin{array}{l}{-\sqrt{3}+b+c=0}\\{-9\sqrt{3}+3b+c=0}\end{array}\right.$,
解:(1)根据题意得:$\left\{\begin{array}{l}{-\sqrt{3}+b+c=0}\\{-9\sqrt{3}+3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=4\sqrt{3}}\\{c=-3\sqrt{3}}\end{array}\right.$,
则抛物线的解析式是y=-$\sqrt{3}$x2+4$\sqrt{3}$x-3$\sqrt{3}$,
y=-$\sqrt{3}$x2+4$\sqrt{3}$x-3$\sqrt{3}$=-$\sqrt{3}$(x2-4x)-3$\sqrt{3}$=-$\sqrt{3}$(x2-4x+4-4)-3$\sqrt{3}$=-$\sqrt{3}$(x-2)2+$\sqrt{3}$,
则顶点D的坐标是(2,$\sqrt{3}$);
(2)在y=-$\sqrt{3}$x2+4$\sqrt{3}$x-3$\sqrt{3}$中令y=0,则-$\sqrt{3}$x2+4$\sqrt{3}$x-3$\sqrt{3}$=0,
解得:x=1或3,则B的坐标是(3,0),
令x=0,则y=-3$\sqrt{3}$,则C的坐标是(0,-3$\sqrt{3}$),
BC=3BE,易得E的坐标是(2,-$\sqrt{3}$).
作EH∥x轴交y轴于点H.
△DFG∽△HFE,
故$\frac{HF}{HE}$=$\frac{2}{\sqrt{3}}$,HE=2.
解得:HF=$\frac{4\sqrt{3}}{3}$,OH=$\sqrt{3}$,OF=$\frac{\sqrt{3}}{3}$,OG=$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$.
S△FEB=S△FGB+S△GEB=$\frac{1}{2}$×(3-$\frac{1}{2}$)×$\frac{\sqrt{3}}{3}$+$\frac{1}{2}$×(3-$\frac{1}{2}$)$\sqrt{3}$=$\frac{1}{2}$×$\frac{5}{2}$×$\frac{4\sqrt{3}}{3}$=$\frac{5\sqrt{3}}{3}$.
即△FEB的面积是$\frac{5\sqrt{3}}{3}$.
(3)∵由题意得△ADB是等边三角形,∠OBC=60°,
∴旋转后B′与A重合,B′P′在x轴上,设线段BP长为d,0<d<6.
P′(1-d,0),B′(1,0),D(2,$\sqrt{3}$).
过D作BP'的垂线,垂足为K,过Q作OB的垂线,垂足为L,由于QOB=NOP'=NP'O,则有△P'DK∽△OQL,
从而得$\frac{OL}{P'K}=\frac{QL}{DK}$,
设Q(a,$-\sqrt{3}(3-a)$),则:$\frac{a}{d+1}=\frac{\sqrt{3}(3-a)}{\sqrt{3}}$;
解得a=$\frac{3(d+1)}{d+2}$,|yQ|=$\frac{3\sqrt{3}}{d+2}$
又P(3-$\frac{d}{2}$,-$\frac{\sqrt{3}}{2}$d),|yP|=$\frac{\sqrt{3}(6-d)}{2}$
则S△PP'Q=S△PP'B-S△BP'Q=$\frac{1}{2}$BP'(|yP|-|yQ|)=$\frac{1}{2}$×(d+2)×($\frac{\sqrt{3}}{2}$d-$\frac{3\sqrt{3}}{d+2}$)=$\frac{\sqrt{3}}{4}$(d2+2d-6)
而易求S△BOC=$\frac{1}{2}×3×3\sqrt{3}$=$\frac{9\sqrt{3}}{2}$
由S△BOC=9S△PP'Q得:$\frac{9\sqrt{3}}{4}$(d2+2d-6)=$\frac{9\sqrt{3}}{2}$,
化简得:d2+2d-6=2;即d2+2d-8=0,
解得d=2或-4(舍去);
故BP的长d=2.
点评 本题考查了待定系数法求函数的解析式以及图形的旋转的性质,注意到△ADB是等边三角形,正确理解B旋转到A的位置,B′P′在x轴上是解题的关键.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | 任意一个正有理数 | B. | 任意一个大于-2015的数 | ||
| C. | 任意一个负数 | D. | 任意一个非正数 |

 在Rt△ABC中,∠C=90°,M是AB的中点,PM⊥MQ.P、Q分别在边AC、BC上.
在Rt△ABC中,∠C=90°,M是AB的中点,PM⊥MQ.P、Q分别在边AC、BC上. 已知FGBA与EDAC为正方形,求证:S△AEF=S△ABC.
已知FGBA与EDAC为正方形,求证:S△AEF=S△ABC. 如图,在数轴上有两点A、B,A表示的数为6,B在A的左侧,且AB=10.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动.
如图,在数轴上有两点A、B,A表示的数为6,B在A的左侧,且AB=10.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动.