题目内容
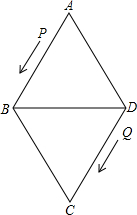
如图,⊙O经过菱形ABCD的三个顶点A、C、D,且与AB相切于点A.

(1)求证:BC为⊙O的切线;
(2)求∠B的度数.
【答案】
(1)证明见解析;(2)∠ABC =60°.
【解析】
试题分析:(1)连结OA、OB、OC、BD,根据切线的性质得OA⊥AB,即∠OAB=90°,再根据菱形的性质得BA=BC,然后根据“SSS”可判断△ABO≌△CBO,则∠BCO=∠BAO=90°,于是可根据切线的判定方法即可得到结论;
(2)由△ABO≌△CBO得∠AOB=∠COB,则∠AOB=∠COB,由于菱形的对角线平分对角,所以点O在BD上,利用三角形外角性质有∠BOC=∠ODC+∠OCD,则∠BOC=2∠ODC,由于CB=CD,∠OBC=∠ODC,所以∠BOC=2∠OBC,根据∠BOC+∠OBC=90°可计算出∠OBC=30°,然后利用∠ABC=2∠OBC计算.
试题解析:(1)连结OA、OB、OC、BD,如图,

∵AB与⊙O切于A点,
∴OA⊥AB,即∠OAB=90°,
∵四边形ABCD为菱形,
∴BA=BC,
在△ABO和△CBO中
 ,
,
∴△ABO≌△CBO(SSS),
∴∠BCO=∠BAO=90°,
∴OC⊥BC,
∴BC为⊙O的切线;
(2)∵△ABO≌△CBO,
∴∠AOB=∠COB,
∵四边形ABCD为菱形,
∴BD平分∠ABC,DA=DC,
∴点O在BD上,
∵∠BOC=∠ODC+∠OCD,OD=OC,
∴∠ODC=∠OCD,
∴∠BOC=2∠ODC,
同理:∠BOC=2∠OBC,
∵∠BOC+∠OBC=90°,
∴∠OBC=30°,
∴∠ABC=2∠OBC=60°.
考点:1.切线的判定与性质,2.菱形的性质.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 点D同时出发沿线路DC→CB→BA作匀速运动.
点D同时出发沿线路DC→CB→BA作匀速运动.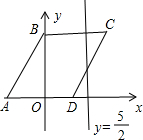 经过B点,且顶点在直线
经过B点,且顶点在直线 (2013•苏州)如图,菱形OABC的顶点C的坐标为(3,4).顶点A在x轴的正半轴上,反比例函数y=
(2013•苏州)如图,菱形OABC的顶点C的坐标为(3,4).顶点A在x轴的正半轴上,反比例函数y= 如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2).反比例函数
如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2).反比例函数