题目内容
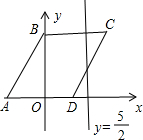
如图,菱形ABCD的顶点A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=| 2 |
| 3 |
 经过B点,且顶点在直线x=
经过B点,且顶点在直线x=| 5 |
| 2 |
(1)求抛物线对应的函数关系式,并说明此抛物线一定过点C、D;
(2)若M点是该抛物线上位于C、D之间的一动点,求△CDM面积的最大值.
分析:(1)把二次函数的解析式化为顶点式y=a(x-h)2+m,因为顶点在直线x=
上,所以h=
,然后再把点B的坐标代入其中求出m的值即可得到二次函数的解析式.再利用A和B的坐标得出线段OA,OB的长,利用勾股定理求出AB,又四边形为菱形得出它的四条边长,从而得出点C和点D的坐标,分别把两点的横坐标代入二次函数的解析式中求出y的值,从而判断出抛物线一定过点C、D.
(2)先利用点C和点D的坐标求出直线CD的解析式,设出M的横坐标为t,因为MN∥y轴,所以N的横坐标也为t,分别把两点的横坐标代入到抛物线和直线CD的解析式中表示出它们的纵坐标,让其纵坐标相减即可得到MN的长l与t的二次函数关系式,求出t=-
=
时MN有最大值为
,然后把MN当作三角形CMN和三角形DMN的公共底,分别表示出三角形CMN和三角形DMN的面积,两三角形面积相加即为三角形CDM的面积,因为三角形CMN和三角形DMN的高之和为定值,所以当三角形的底MN取最大值时三角形CDM的面积最大.
| 5 |
| 2 |
| 5 |
| 2 |
(2)先利用点C和点D的坐标求出直线CD的解析式,设出M的横坐标为t,因为MN∥y轴,所以N的横坐标也为t,分别把两点的横坐标代入到抛物线和直线CD的解析式中表示出它们的纵坐标,让其纵坐标相减即可得到MN的长l与t的二次函数关系式,求出t=-
| b |
| 2a |
| 7 |
| 2 |
| 3 |
| 2 |
解答: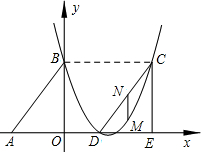 解:(1)由题意,可设所求抛物线对应的函数关系式为y=
解:(1)由题意,可设所求抛物线对应的函数关系式为y=
(x-
)2+m,
∴4=
×(-
)2+m,
∴m=-
,(2分)
∴所求函数关系式为:y=
(x-
)2-
=
x2-
x+4,
在Rt△ABO中,OA=3,OB=4,
∴AB=
=5,
∵四边形ABCD是菱形,
∴BC=CD=DA=AB=5,
∴C、D两点的坐标分别是(5,4)、(2,0).
当x=5时,y=
×52-
×5+4=4,
当x=2时,y=
×22-
×2+4=0,
∴点C和点D在所求抛物线上;
(2)设直线CD对应的函数关系式为y=kx+b,则
,
解得:k=
,b=-
.
∴y=
x-
,(6分)
∵MN∥y轴,M点的横坐标为t,
∴N点的横坐标也为t.
则yM=
t2-
t+4,yN=
t-
,
∴l=yN-yM=
t-
-(
t2-
t+4)=-
t2+
t-
=-
(t-
)2+
,
∵-
<0,
∴当t=
时,l最大=
,
 解:(1)由题意,可设所求抛物线对应的函数关系式为y=
解:(1)由题意,可设所求抛物线对应的函数关系式为y=| 2 |
| 3 |
| 5 |
| 2 |
∴4=
| 2 |
| 3 |
| 5 |
| 2 |
∴m=-
| 1 |
| 6 |
∴所求函数关系式为:y=
| 2 |
| 3 |
| 5 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
| 10 |
| 3 |
在Rt△ABO中,OA=3,OB=4,
∴AB=
| OA2+OB2 |
∵四边形ABCD是菱形,
∴BC=CD=DA=AB=5,
∴C、D两点的坐标分别是(5,4)、(2,0).
当x=5时,y=
| 2 |
| 3 |
| 10 |
| 3 |
当x=2时,y=
| 2 |
| 3 |
| 10 |
| 3 |
∴点C和点D在所求抛物线上;
(2)设直线CD对应的函数关系式为y=kx+b,则
|
解得:k=
| 4 |
| 3 |
| 8 |
| 3 |
∴y=
| 4 |
| 3 |
| 8 |
| 3 |
∵MN∥y轴,M点的横坐标为t,
∴N点的横坐标也为t.
则yM=
| 2 |
| 3 |
| 10 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
∴l=yN-yM=
| 4 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 10 |
| 3 |
| 2 |
| 3 |
| 14 |
| 3 |
| 20 |
| 3 |
| 2 |
| 3 |
| 7 |
| 2 |
| 3 |
| 2 |
∵-
| 2 |
| 3 |
∴当t=
| 7 |
| 2 |
| 3 |
| 2 |
|
点评:本题是二次函数的综合题型,其中涉及到的知识点有菱形的性质和三角形的面积求法.本题的难点是第二问,学生要弄懂△CDM面积的最大值满足的条件.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
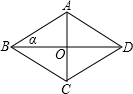 如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )
如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )A、sinα=
| ||
B、cosα=
| ||
C、tanα=
| ||
D、tanα=
|
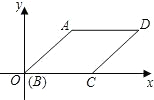 如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为
如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为 如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.
如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.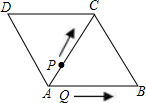 △ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
△ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).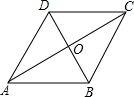 已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.
已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.