题目内容
7.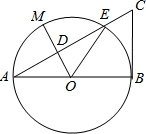 如图,以线段AB为直径的⊙O交线段AC于点E,点M是$\widehat{AE}$ 的中点,OM交AC于点D,BC=2$\sqrt{3}$,∠BOE=60°,∠C=60°.
如图,以线段AB为直径的⊙O交线段AC于点E,点M是$\widehat{AE}$ 的中点,OM交AC于点D,BC=2$\sqrt{3}$,∠BOE=60°,∠C=60°.(1)求∠A的度数;
(2)求证:BC是⊙O的切线;
(3)求MD的长度.
分析 (1)根据圆周角定理计算;
(2)根据三角形内角和定理求出∠ABC=90°,根据切线的判定定理证明;
(3)根据垂径定理得到OM⊥AE,求出圆的半径,计算即可.
解答 (1)解:∵∠BOE=60°,
∴∠A=$\frac{1}{2}$∠BOE=30°;
(2)证明:在△ABC中,∵∠C=60°,∠A=30°,
∴∠ABC=90°,
∴AB⊥BC,
又∵OB为⊙O的半径,
∴BC是⊙O的切线;
(3)解:∵点M是 AE 的中点,
∴OM⊥AE,
在Rt△ABC中,BC=2$\sqrt{3}$,∠A=30°,
∴AC=4$\sqrt{3}$,
∴AB=6,
∴OA=$\frac{1}{2}$AB=3,
∴OD=$\frac{1}{2}$OA=$\frac{3}{2}$,
∴MD=OM-OD=$\frac{3}{2}$.
点评 本题考查的是切线的判定、垂径定理的应用、锐角三角函数的定义,掌握切线的判定定理是解题的关键.

练习册系列答案
相关题目
12.若ax=6,ay=4,则a2x-y的值为( )
| A. | 8 | B. | 9 | C. | 32 | D. | 40 |
16.将抛物线y=-2(x+1)2-2向左平移2个单位,向下平移3个单位后的新抛物线解析式为( )
| A. | y=-2(x-1)2+1 | B. | y=-2(x+3)2-5 | C. | y=-2(x-1)2-5 | D. | y=-2(x+3)2+1 |
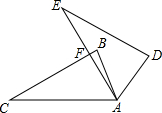 如图,△ABC中,∠C=30°,将△ABC绕点A顺时针旋转50°得到△ADE,AE与BC交于F,则∠AFB=80°.
如图,△ABC中,∠C=30°,将△ABC绕点A顺时针旋转50°得到△ADE,AE与BC交于F,则∠AFB=80°.