题目内容
8.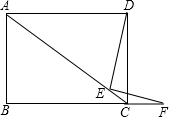 如图:四边形ABCD为矩形,E在对角线AC上,F在边BC的延长线上,且$\frac{DE}{EF}$=$\frac{BC}{AB}$,求证:DE⊥EF.
如图:四边形ABCD为矩形,E在对角线AC上,F在边BC的延长线上,且$\frac{DE}{EF}$=$\frac{BC}{AB}$,求证:DE⊥EF.
分析 作EM⊥BC于M,EN⊥CD于N,由四边形ABCD是矩形,得到∠B=∠ADC=DCB=90°,AD=BC,由于EM∥AB,EN∥AD,推出△CEM∽△CAB,△CEN∽△CAD,得到$\frac{EM}{AB}=\frac{CE}{CA}$,$\frac{CE}{CA}=\frac{EN}{AD}$,等量代换得到$\frac{EM}{AB}=\frac{EN}{AD}$,根据比例的性质得到$\frac{EM}{EN}=\frac{AB}{AD}$,于是推出$\frac{EM}{EN}=\frac{EF}{DE}$.证得Rt△FEM∽Rt△DEN,得到∠EFM∠EDN,于是得到E,C,F,D四点共圆,即可得到结论.
解答  解:作EM⊥BC于M,EN⊥CD于N,
解:作EM⊥BC于M,EN⊥CD于N,
∵四边形ABCD是矩形,
∴∠B=∠ADC=DCB=90°,AD=BC,
∴EM∥AB,EN∥AD,
∴△CEM∽△CAB,△CEN∽△CAD,
∴$\frac{EM}{AB}=\frac{CE}{CA}$,$\frac{CE}{CA}=\frac{EN}{AD}$,
∴$\frac{EM}{AB}=\frac{EN}{AD}$,
∴$\frac{EM}{EN}=\frac{AB}{AD}$,
∵AD=BC,
∴$\frac{EM}{EN}=\frac{AB}{BC}$,
∴$\frac{EM}{EN}=\frac{EF}{DE}$.
∴Rt△FEM∽Rt△DEN,
∴∠EFM∠EDN,
∴E,C,F,D四点共圆,
∴∠DEF=∠DCF=90°,
∴DE⊥EF.
点评 本题考查了相似三角形的判定和性质,四点共圆,矩形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
15.如果分式$\frac{1}{{x}^{2}+x-1}$有意义,则( )
| A. | x≠1-$\sqrt{5}$ | B. | x≠$\frac{1-\sqrt{5}}{2}$ | C. | x≠-1±$\sqrt{5}$ | D. | x≠$\frac{-1±\sqrt{5}}{2}$ |
13.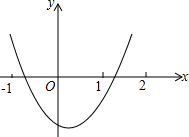 二次函数y=ax2+bx+c的图象如图,下列不等关系中分析错误的是( )
二次函数y=ax2+bx+c的图象如图,下列不等关系中分析错误的是( )
 二次函数y=ax2+bx+c的图象如图,下列不等关系中分析错误的是( )
二次函数y=ax2+bx+c的图象如图,下列不等关系中分析错误的是( )| A. | 3a+b>0 | B. | a+b+2c<0 | C. | 4a+b+c>0 | D. | a-3b+c<0 |
17.不等式2x+1<5的正整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
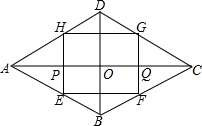 如图,在菱形ABCD中,两条对角线长是AC=10,BD=6,F是线段AO上一点(不与A、O重合),Q是线段OC上一点,且AP=CQ,分别将∠BAD和∠BCD折叠,使A、C两点都在对角线AC上,折痕分别是EH和FG,EH过P点,FG过Q点,连接EF、HG,再把折叠部分铺平.
如图,在菱形ABCD中,两条对角线长是AC=10,BD=6,F是线段AO上一点(不与A、O重合),Q是线段OC上一点,且AP=CQ,分别将∠BAD和∠BCD折叠,使A、C两点都在对角线AC上,折痕分别是EH和FG,EH过P点,FG过Q点,连接EF、HG,再把折叠部分铺平.