题目内容
13.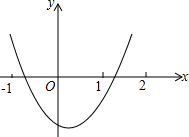 二次函数y=ax2+bx+c的图象如图,下列不等关系中分析错误的是( )
二次函数y=ax2+bx+c的图象如图,下列不等关系中分析错误的是( )| A. | 3a+b>0 | B. | a+b+2c<0 | C. | 4a+b+c>0 | D. | a-3b+c<0 |
分析 由抛物线开口向上得出a>0,与y轴交于负半轴c<0,由对称轴0<-$\frac{b}{2a}$<1,可得b<0,b>-2a,当x=-1或1或2对应的函数值逐一探讨得出答案即可.
解答 解:∵抛物线开口向上得出a>0,对称轴0<-$\frac{b}{2a}$<1,
∴2a+b>0.
∴3a+b>0.(故选项A正确)
∵与y轴交于负半轴c<0,当x=1时,a+b+c<0,
∴a+b+2c<0.(故选项B正确)
∵由函数图象可知,当x=2时,4a+2b+c>0,
∴4a+b+c>-b.
∵a>0,$-\frac{b}{2a}>0$,
∴b<0.
∴-b>0.
∴4a+b+c>-b>0.(故选项C正确)
∵由函数图象可知,当x=-1时,a-b+c>0,
又∵-b>0,
∴a-3b+c>0.(故选项D错误)
故选D.
点评 本题考查二次函数图象与系数之间的关系,关键是根据图象和二次函数的特点,灵活变化,求出问题中的结论正确与否.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
5.按如图方式摆放餐桌和椅子

(1)1张餐桌可坐6个人,2张餐桌可坐8人;
(2)按照上图的方式继续排列餐桌,完成表:

(1)1张餐桌可坐6个人,2张餐桌可坐8人;
(2)按照上图的方式继续排列餐桌,完成表:
| 桌子张数 | 4 | 5 | … | n |
| 可坐人数 | 12 | 14 | … | 4+2n |
2.下列代数式中,全是单项式的一组是( )
| A. | $\frac{1}{a},2,\frac{ab}{3}$ | B. | $2,a,\frac{1}{2}ab$ | C. | $\frac{a-b}{2},1,π$ | D. | $x+y,-4,\frac{1}{2}(x-y)$ |
3.若x=m时,代数式x2-x-1的值为2.则代数式m2-m+2011的值为( )
| A. | 4 | B. | 2009 | C. | 2014 | D. | 3 |
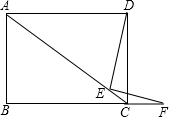 如图:四边形ABCD为矩形,E在对角线AC上,F在边BC的延长线上,且$\frac{DE}{EF}$=$\frac{BC}{AB}$,求证:DE⊥EF.
如图:四边形ABCD为矩形,E在对角线AC上,F在边BC的延长线上,且$\frac{DE}{EF}$=$\frac{BC}{AB}$,求证:DE⊥EF.