题目内容
4.下列一元二次方程没有实数根的是( )| A. | x2-9=0 | B. | x2-x-1=0 | C. | -x2+3x-$\frac{9}{4}$=0 | D. | x2+x+1=0 |
分析 分别求出各个一元二次方程的根的判别式,再作出判断即可.
解答 解:A、x2-9=0有两个相等的根,此选项错误;
B、x2-x-1=0,△=5,方程有两个不相等的实数根,此选项错误;
C、-x2+3x-$\frac{9}{4}$=0,△=9-4×(-1)×(-$\frac{9}{4}$)=0,方程有两个相等的实数根,此选项错误;
D、x2+x+1=0,△=1-4=-3<0,方程没有实数根,此选项正确;
故选D.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.数轴上的点A表示数为1,则数轴上到点A的距离为2的点表示的数为( )
| A. | 2 | B. | 3 | C. | -1 | D. | -1或3 |
12.化简-|-(+5)|,结果正确的是( )
| A. | 5 | B. | -5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
13. 如图,下列条件中,能得到DG∥BC的是( )
如图,下列条件中,能得到DG∥BC的是( )
 如图,下列条件中,能得到DG∥BC的是( )
如图,下列条件中,能得到DG∥BC的是( )| A. | CD⊥AB,EF⊥AB | B. | ∠1=∠2 | ||
| C. | ∠1=∠2,∠4+∠5=180° | D. | CD⊥AB,EF⊥AB,∠1=∠2 |
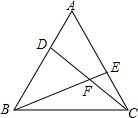 如图,点D、E分别在等边△ABC的AB、AC边上,BE与CD交于F,∠BFC=120°,求证:AD=CE.
如图,点D、E分别在等边△ABC的AB、AC边上,BE与CD交于F,∠BFC=120°,求证:AD=CE.