题目内容
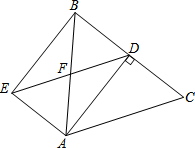
8．
如图，AB∥CD，AF∥CG，则图中与∠A（不包括∠A）相等的角有（ ）| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
分析 由AB∥CD结合“两直线平行，内错角相等”可得出∠A=∠ADC，再由AF∥CG结合“两直线平行，内错角相等”可得出∠C=∠ADC，由此即可得出结论．
解答 解：∵AB∥CD，
∴∠A=∠ADC．
∵AF∥CG，
∴∠C=∠ADC=∠A．
∴图中与∠A（不包括∠A）相等的角有2个．
故选A．
点评 本题考查了平行线的性质，解题的关键是根据两直线平行找出相等的角．本题属于基础题，难度不大，解决该题型题目时，根据平行线的性质找出相等（或互补）的角是关键．
练习册系列答案
相关题目
18．下列计算结果正确的是（ ）
| A． | （-a3）2=a9 | B． | a6÷a3=a2 | C． | （-$\frac{1}{2}$）-1=-2 | D． | （cos60°-$\frac{1}{2}$）0=1 |
如图，在△ABC中，AB=AC=5，BC=6，AD为BC边上的高，过点A作AE∥BC，过点D作DE∥AC，AE与DE交于点E，AB与DE交于点F，连结BE．
20．下列说法正确的是（ ）
| A． | -1的倒数是1 | B． | -1的相反数是-1 | ||
| C． | 1的立方根是±1 | D． | 1的算术平方根是1 |
若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是π+$\frac{\sqrt{3}}{3}$．