题目内容
8.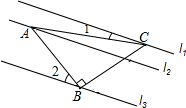 如图所示,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点分别在相互平行的三条直线l1、l2、l3上,且∠1=15°,则∠2=30度.
如图所示,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点分别在相互平行的三条直线l1、l2、l3上,且∠1=15°,则∠2=30度.
分析 由l1∥l2∥l3可以得出∠1=∠3,∠2=∠4,由等腰直角三角形的性质就可以得出∠BAC=45°,就可以得出∠1+∠2=∠3+∠4.就可以求出∠2的值.
解答  解:∵l1∥l2∥l3,
解:∵l1∥l2∥l3,
∴∠1=∠3,∠2=∠4,
∴∠1+∠2=∠3+∠4.
∵∠ABC=90°,AB=BC,
∴∠BAC=∠BCA=45°.
∵∠3+∠4=∠BAC,
∴∠3+∠4=45°,
∴∠1+∠2=45°.
∵∠1=15°,
∴∠2=30°.
故答案为:30.
点评 本题考查了平行线的性质,等式的性质的运用,等腰直角三角形的性质的运用,解答时根据平行线的性质求解是关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
19.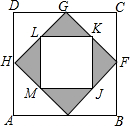 如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,顺次连接四边形EFGH各边的中点得到四边形JKLM,若向正方形ABCD中随机撒一粒豆子,则它落在阴影部分的概率是( )
如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,顺次连接四边形EFGH各边的中点得到四边形JKLM,若向正方形ABCD中随机撒一粒豆子,则它落在阴影部分的概率是( )
 如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,顺次连接四边形EFGH各边的中点得到四边形JKLM,若向正方形ABCD中随机撒一粒豆子,则它落在阴影部分的概率是( )
如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,顺次连接四边形EFGH各边的中点得到四边形JKLM,若向正方形ABCD中随机撒一粒豆子,则它落在阴影部分的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
3.观察下列各数:1,$\frac{4}{3}$,$\frac{9}{7}$,$\frac{16}{15}$,…,按你发现的规律计算这列数的第6个数为( )
| A. | $\frac{25}{31}$ | B. | $\frac{36}{35}$ | C. | $\frac{4}{7}$ | D. | $\frac{62}{63}$ |
13.标号为A、B、C、D的四个盒子中所装有白球和黑球数如下,则下列盒子最易摸到黑球的是( )
| A. | 9个黑球和3个白球 | B. | 10黑球和10个白球 | ||
| C. | 12个黑球和6个白球 | D. | 10个黑球和5个白球 |
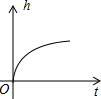
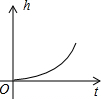
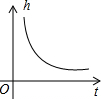
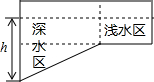 某游泳池横截面如图所示,用一水管向池内持续注水,若单位时间内注入的水量保持不变,则在注水过程中,下列图象能反应深水区水深h与注水时间t关系的是( )
某游泳池横截面如图所示,用一水管向池内持续注水,若单位时间内注入的水量保持不变,则在注水过程中,下列图象能反应深水区水深h与注水时间t关系的是( )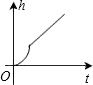




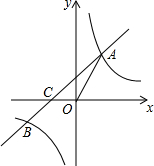 如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A和点B(-2,n),与x轴交于点C(-1,0),连接OA.
如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A和点B(-2,n),与x轴交于点C(-1,0),连接OA.