题目内容
某项工程若由甲乙两队分别单独完成,则甲队用时是乙队的1.5倍;若由甲乙两人合作,则需12天完成.
(1)甲乙两队单独完成各需多少天?
(2)若施工方案是甲先单独施工x天,剩下工程甲、乙合作完成,若甲队施工费用为每天1万元,乙队施工费用为每天2.5万元,求施工总费用y(万元)与施工时间x(天)的函数关系式;
(3)在(2)的方案下,若施工期定为15~18天内完成(含15和18天),如何安排施工方案使费用最少,最少费用为多少万元?
(1)甲乙两队单独完成各需多少天?
(2)若施工方案是甲先单独施工x天,剩下工程甲、乙合作完成,若甲队施工费用为每天1万元,乙队施工费用为每天2.5万元,求施工总费用y(万元)与施工时间x(天)的函数关系式;
(3)在(2)的方案下,若施工期定为15~18天内完成(含15和18天),如何安排施工方案使费用最少,最少费用为多少万元?
考点:一次函数的应用,分式方程的应用,一元一次不等式组的应用
专题:
分析:(1)设乙单独完成需a天,则甲单独完成需1.5a天,然后根据合作12天完成,利用甲、乙两队的工作效率之和列出方程求解即可;
(2)设甲乙合作完成余下部分所需时间为w天,根据两队的工作量之和等于总工作量“1”列出方程用x表示出w,再根据施工总费用等于两队的费用之和列式整理即可得解;
(3)根据施工期列出不等式组求出x的取值范围,再根据一次函数的增减性求出费用最少值即可.
(2)设甲乙合作完成余下部分所需时间为w天,根据两队的工作量之和等于总工作量“1”列出方程用x表示出w,再根据施工总费用等于两队的费用之和列式整理即可得解;
(3)根据施工期列出不等式组求出x的取值范围,再根据一次函数的增减性求出费用最少值即可.
解答:解:(1)设乙单独完成需a天,则甲单独完成需1.5a天,
根据题意列:
+
=
,
解得,a=20,
经检验:a=20是所列方程根,且符合题意,
所以1.5a=30,
答:甲、乙两队单独完成分别需30天,20天;
(2)设甲乙合作完成余下部分所需时间为w天,列:
+
+
=1,
解得,w=-
x+12,
∴y=x+(1+2.5)(-
x+12)=-
x+42;
(3)由题可得15≤x-
x+12≤18,
解得,5≤x≤10,
∵-
<0,
∴y随x的增大而减小,
∴当x=10时,y最小=-
×10+42=38,
此时,甲先施工10天,再甲乙合作8天,费用最低为38万元.
根据题意列:
| 1 |
| a |
| 1 |
| 1.5a |
| 1 |
| 12 |
解得,a=20,
经检验:a=20是所列方程根,且符合题意,
所以1.5a=30,
答:甲、乙两队单独完成分别需30天,20天;
(2)设甲乙合作完成余下部分所需时间为w天,列:
| x |
| 30 |
| w |
| 30 |
| w |
| 20 |
解得,w=-
| 2 |
| 5 |
∴y=x+(1+2.5)(-
| 2 |
| 5 |
| 2 |
| 5 |
(3)由题可得15≤x-
| 2 |
| 5 |
解得,5≤x≤10,
∵-
| 2 |
| 5 |
∴y随x的增大而减小,
∴当x=10时,y最小=-
| 2 |
| 5 |
此时,甲先施工10天,再甲乙合作8天,费用最低为38万元.
点评:本题考查了一次函数的应用,分式方程的应用,一元一次不等式组的应用,熟练掌握工作量问题并找出等量关系和不等关系是解题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 如图,在△ABC,DE∥BC,若
如图,在△ABC,DE∥BC,若| AD |
| AB |
| 1 |
| 2 |
| A、8 | ||
| B、10 | ||
C、
| ||
| D、12 |
 如图,一次函数y=-
如图,一次函数y=-
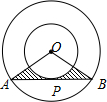 如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6、3,则图中阴影部分的面积是
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6、3,则图中阴影部分的面积是