Question

【题目】已知如图，BQ平分∠ABP，CQ平分∠ACP，∠BAC＝α，∠BPC＝β，则∠BQC＝_________．（用α，β表示）

Answer 1

【答案】(α+β)．

【解析】

连接BC，根据角平分线的性质得到∠3=∠ABP，∠4=∠ACP，根据三角形的内角和得到∠1+∠2=180°-β，2（∠3+∠4）+（∠1+∠2）=180°-α，求出∠3+∠4=（β-α），根据三角形的内角和即可得到结论．

解：连接BC，

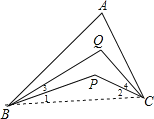
∵BQ平分∠ABP，CQ平分∠ACP，

∴∠3=∠ABP，∠4=∠ACP，

∵∠1+∠2=180°-β，2（∠3+∠4）+（∠1+∠2）=180°-α，

∴∠3+∠4=（β-α），
∵∠BQC=180°-（∠1+∠2）-（∠3+∠4）=180°-（180°-β）-（β-α），
即：∠BQC=（α+β）．
故答案为：（α+β）．