题目内容
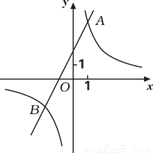
已知反比例函数的图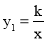 象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知反比例函数的图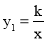 象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案