题目内容
14.一个长方体的体积是200cm3,它的长是y cm,宽是5cm,高是x cm.(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)求$\frac{1}{2}$≤x≤12时,y的最大值和最小值.
分析 (1)利用立方体的体积公式得出y与x的函数关系式,进而得出x的取值范围;
(2)分别求出x=$\frac{1}{2}$以及x=12时y的值进而得出答案.
解答 解:(1)依题意,得5xy=200,
∴y=$\frac{40}{x}$,
又∵x是长方体的高,
∴x>0,即自变量x的取值范围是:x>0;
(2)∵当x=$\frac{1}{2}$时,y=$\frac{40}{\frac{1}{2}}$=80;
当x=12时,y=$\frac{40}{12}$=$\frac{10}{3}$.
∴在$\frac{1}{2}$≤x≤12时,长方体的长最大值是80cm,最小值是$\frac{10}{3}$cm.
点评 此题主要考查了反比例函数的应用,根据长方体体积公式得出y与x的函数关系式是解题关键.

练习册系列答案
相关题目
4.在△ABC中,D,E分别是AB,AC上的点,且DE∥BC,则下列结论不正确的是( )
| A. | $\frac{AD}{DB}$=$\frac{AE}{EC}$ | B. | $\frac{AB}{DB}$=$\frac{AC}{EC}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{AD}{DB}$=$\frac{AC}{BC}$ |
2. 如图,已知45°<∠A<90°,则下列各式成立的是( )
如图,已知45°<∠A<90°,则下列各式成立的是( )
 如图,已知45°<∠A<90°,则下列各式成立的是( )
如图,已知45°<∠A<90°,则下列各式成立的是( )| A. | sinA=cosA | B. | sinA>cosA | C. | sinA>tanA | D. | sinA<cosA |




 如图,△ABC的三个顶点在⊙O上,AD是△ABC的高,AE是⊙O的直径,求证:∠1=∠2.
如图,△ABC的三个顶点在⊙O上,AD是△ABC的高,AE是⊙O的直径,求证:∠1=∠2.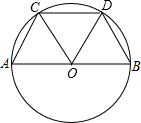 如图,AB是⊙O的直径,如果∠COA=∠DOB=60°,那么与线段OA相等的线段有AC,OC,CD,OD,BD,OB,与$\widehat{AC}$相等的弧有$\widehat{CD}$,$\widehat{BD}$.
如图,AB是⊙O的直径,如果∠COA=∠DOB=60°,那么与线段OA相等的线段有AC,OC,CD,OD,BD,OB,与$\widehat{AC}$相等的弧有$\widehat{CD}$,$\widehat{BD}$.