如图.△ABC的三个顶点在⊙O上.AD是△ABC的高.AE是⊙O的直径.求证:∠1=∠2．题目和参考答案——青夏教育精英家教网—

题目内容

19．

如图，△ABC的三个顶点在⊙O上，AD是△ABC的高，AE是⊙O的直径，求证：∠1=∠2．

分析首先连接BE，由AE是⊙O的直径，AD是△ABC的高，可得∠1+∠E=90°，∠2+∠C=90°，又由圆周角定理，可证得∠C=∠E，继而证得结论．

解答证明：连接BE，
∵AE是⊙O的直径，
∴∠ABE=90°，
∴∠1+∠E=90°，
∵AD⊥BC，
∴∠2+∠C=90°，
∵∠C=∠E，
∴∠1=∠2．

点评此题考查了圆周角定理．注意掌握辅助线的作法，注意直径对的圆周角是直角．

练习册系列答案

相关题目

9．

如图，如果∠B=∠C，那么△BAE∽△CAD，△BOD∽△COE．

10．下列结论正确的是（　　）

	A．	经过圆心的直线是圆的对称轴		B．	直径是圆的对称轴
	C．	与圆相交的直线是圆的对称轴		D．	与直径相交的直线是圆的对称轴

7．下列坐标中，在直线y=x上的点的坐标是（　　）

14．一个长方体的体积是200cm³，它的长是y cm，宽是5cm，高是x cm．
（1）求y与x的函数关系式，并写出自变量x的取值范围；
（2）求$\frac{1}{2}$≤x≤12时，y的最大值和最小值．

4．

如图，OA，OB，OC，OD是⊙O的半径，
（1）如果∠AOB=∠COD，那么AB=CD，$\widehat{AB}$=$\widehat{CD}$，∠AOC=∠BOD；（2）如果AB=CD，那么$\widehat{AB}$=$\widehat{CD}$，∠AOB=∠COD；
（3）如果$\widehat{AB}$=$\widehat{CD}$，那么AB=CD，∠AOB=∠COD，$\widehat{AC}$=$\widehat{BD}$．

11．一个扇形的圆心角为60°，它所对的弧长为2πcm，则这个扇形的半径为（　　）

8．

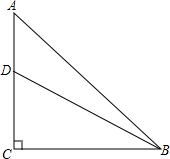如图，在等腰Rt△ABC中，∠C=90°，AC=6，D是AC上一点，若tan∠DBA=$\frac{1}{5}$，则AD的长为（　　）

9．

某班实行小组量化考核制，为了了解同学们的学习情况，王老师对甲、乙两个小组连续六周的综合评价得分进行了统计，并将得到的数据制成如下的统计表：

周次
组别	一	二	三	四	五	六
甲组	12	15	16	14	14	13
乙组	9	14	10	17	16	18

（1）请根据上表中的数据完成下表；（注：方差的计算结果精确到0.1）
（2）根据综合评价得分统计表中的数据，请在图中画出甲、乙两组综合评价得分的折线统计图；
（3）由折线统计图中的信息，请分别对甲、乙两个小组连续六周的学习情况做出简要评价．

	平均数	中位数	方差
甲组	14	14	1.7
乙组	14	15	11.7

试题分类