题目内容
4.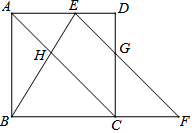 如图,在正方形ABCD中,E是AD边上的动点(与A、D不重合),点F在边BC的延长线上,且AE=CF,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H.
如图,在正方形ABCD中,E是AD边上的动点(与A、D不重合),点F在边BC的延长线上,且AE=CF,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H.(1)求证:EF∥AC;
(2)若 BE=EG,求∠BEF大小;
(3)求证:tan∠ABE=$\frac{GF}{AH}$-1.
分析 (1)根据有一组对边平行且相等的四边形是平行四边形即可判定.
(2)先确定△GCF是等腰直角三角形,得出CG=AE,然后通过△BAE≌△BCG,得出BE=BG=EG,即可求得.
(3)由△BAE≌△BCG知∠ABE=∠CBG,结合∠BAC=∠F=45°证△AHB∽△FGB得$\frac{AH}{GF}$=$\frac{AB}{BF}$=$\frac{1}{\frac{BF}{AB}}$=$\frac{1}{\frac{BC+CF}{AB}}$=$\frac{1}{\frac{AB+AE}{AB}}$=$\frac{1}{1+\frac{AE}{AB}}$=$\frac{1}{1+tan∠ABE}$,即可求得.
解答 解:(1)∵四边形ABCD是正方形,
∴AE∥CF,
又∵AE=CF,
∴四边形AEFC是平行四边形,
故EF∥AC.
(2)连接BG,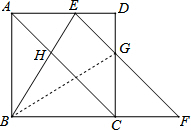
∵四边形ABCD是正方形,且EF∥AC,
∴∠DEG=∠DAC=45°,∠DGE=∠DCA=45°;
故∠CFG=∠DEG=45°,∠CGF=∠DGE=45°,
∴∠CGF=∠CFG,CG=CF;
∵AE=CF,
∴AE=CG;
在△ABE与△CBG中,
∵$\left\{\begin{array}{l}{AB=BC}\\{∠EAB=∠GCB}\\{AE=CG}\end{array}\right.$,
∴△ABE≌CBG(SAS),
∴BE=BG;
又∵BE=EG,
∴BE=BG=EG,△BEG是等边三角形,
故∠BEF=60°.
(3)∵△BAE≌△BCG,
∴∠ABE=∠CBG,
∵∠BAC=∠F=45°,
∴△AHB∽△FGB,
∴$\frac{AH}{GF}$=$\frac{AB}{BF}$=$\frac{1}{\frac{BF}{AB}}$=$\frac{1}{\frac{BC+CF}{AB}}$=$\frac{1}{\frac{AB+AE}{AB}}$=$\frac{1}{1+\frac{AE}{AB}}$=$\frac{1}{1+tan∠ABE}$,
∴1+tan∠ABE=$\frac{GF}{AH}$,即tan∠ABE=$\frac{GF}{AH}$-1.
点评 本题考查了平行四边形的判定及性质,全等三角形的判定及性质,正方形的性质,相似三角形的判定及性质,连接BG是本题的关键.

 智能训练练测考系列答案
智能训练练测考系列答案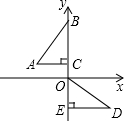 如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| B. | △ABC绕点C逆时针旋转90°,再向下平移3 | |
| C. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C顺时针旋转90°,再向下平移3 |
| A. | 3(x-1)-4x+3=1 | B. | 3x-1-4x+3=6 | C. | 3x-1-4x+3=1 | D. | 3(x-1)-2(2x+3)=6 |
| A. | y=x2-2 | B. | y=(x-2)2 | C. | y=x2+2 | D. | y=(x+2)2 |
| A. | k<9且k≠0 | B. | k<9 | C. | k≤9且k≠0 | D. | k≥9 |

 某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示)
某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示) 某台阶如图,现要在台阶上铺地毯,那么至少需要地毯4.1米.
某台阶如图,现要在台阶上铺地毯,那么至少需要地毯4.1米.