题目内容
1.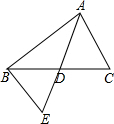 如图,△ABC中,AD是中线,将△ACD旋转后能与△EBD重合.
如图,△ABC中,AD是中线,将△ACD旋转后能与△EBD重合.(1)旋转中心是点D,旋转了180度;
(2)如果AB=5,AC=3,求中线AD长的取值范围.
分析 (1)根据旋转的性质填空即可;
(2)根据三角形的任意两边之和大于第三边,两边之差小于第三边求出AE的取值范围,再根据旋转的性质可得DE=AD,然后求解即可.
解答 解:(1)∵将△ACD旋转后能与△EBD重合,
∴旋转中心是点D,旋转了180度;
故答案为:D,180;
(2)∵将△ACD旋转后能与△EBD重合,
∴BE=AC=3,DE=AD,
在△ABE中,由三角形的三边关系得,AB-BE<AE<AB+BE,
∵AB=5,
∴2<AE<8,
∴1<AD<4,
即中线AD长的取值范围是1<AD<4.
点评 本题考查了旋转的性质,三角形的三边关系,熟记各性质并准确识图是解题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
12.如图标志中,可以看作是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9. 中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为( )
中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为( )
 中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为( )
中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为( )| A. | 9 | B. | 6 | C. | 5 | D. | $\frac{9}{2}$ |
5.有一个数值转换器,原理如图,当输入的x=64时,输出的y等于( )


| A. | 2 | B. | 8 | C. | $\sqrt{8}$ | D. | $\sqrt{18}$ |
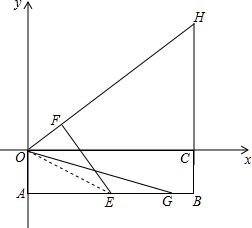 如图,矩形OABC中,OA在y轴的负半轴上,OC在x轴的正半轴上,OA=1,OC=4,E是AB的中点,将矩形沿OE折叠,点A与点F重合,延长OF、BC交于点H,G是射线AB上一点,将△OAG绕点O旋转,使得点A落在OE上,记旋转后的三角形为△OA′G′,A′G′与OH交于点M,若∠MHG′=∠MHB,则AG的长为$\frac{2+20\sqrt{5}}{11}$.
如图,矩形OABC中,OA在y轴的负半轴上,OC在x轴的正半轴上,OA=1,OC=4,E是AB的中点,将矩形沿OE折叠,点A与点F重合,延长OF、BC交于点H,G是射线AB上一点,将△OAG绕点O旋转,使得点A落在OE上,记旋转后的三角形为△OA′G′,A′G′与OH交于点M,若∠MHG′=∠MHB,则AG的长为$\frac{2+20\sqrt{5}}{11}$.