题目内容
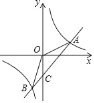
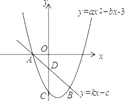
【题目】如图,在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A、
与x轴交于点A、![]() 在B左侧
在B左侧![]() ,与y轴交于点C,经过点A的射线AF与y轴正半轴相交于点E,与抛物线的另一个交点为F,
,与y轴交于点C,经过点A的射线AF与y轴正半轴相交于点E,与抛物线的另一个交点为F,![]() ,点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且
,点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且![]() ,则点P的坐标是______.
,则点P的坐标是______.
【答案】![]() 或
或![]()
【解析】
过点F作![]() 轴,垂足为
轴,垂足为![]() 设
设![]() ,则
,则![]() ,则
,则![]() ,将点F的坐标代入抛物线的解析式可求得t的值,最后,依据
,将点F的坐标代入抛物线的解析式可求得t的值,最后,依据![]() 的值;然后求得
的值;然后求得![]() ,则
,则![]() 当点P在AF的上方时可证明
当点P在AF的上方时可证明![]() ,从而可求得点P的坐标;当点P在AF的下方时,设FP与x轴交点为
,从而可求得点P的坐标;当点P在AF的下方时,设FP与x轴交点为![]() ,则
,则![]() ,可得到
,可得到![]() ,从而可求得m的值,然后再求得PF的解析式,从而可得到点P的坐标.
,从而可求得m的值,然后再求得PF的解析式,从而可得到点P的坐标.
解:过点F作![]() 轴,垂足为M.
轴,垂足为M.
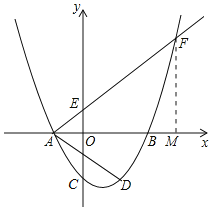
设![]() ,则
,则![]() .
.
![]() ,
,
![]() .
.
![]() .
.
将点![]() 代入
代入![]() 得:
得:![]() ,解得
,解得![]() .
.
![]() .
.
![]() .
.
![]() ,
,![]() .
.
易得抛物线的对称轴为![]() ,
,![]() .
.
![]() 点D是点C关于抛物线对称轴的对称点,
点D是点C关于抛物线对称轴的对称点,
![]() .
.
![]() ,
,
![]() .
.
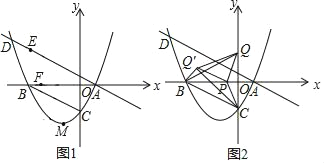
如下图所示:
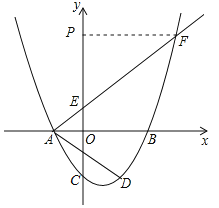
当点P在AF的上方时,![]() ,
,
![]() ,
,
![]() .
.
由![]() 可知:
可知:![]() ,
,![]() .
.
![]() .
.
![]() 点P的坐标为
点P的坐标为![]() .
.
当点P在AF的下方时,如下图所示:
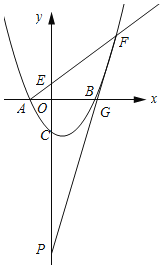
设FP与x轴交点为![]() ,则
,则![]() ,可得到
,可得到![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() .
.
设PF的解析式为![]() ,将点F和点G的坐标代入得:
,将点F和点G的坐标代入得: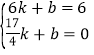 ,
,
解得:![]() ,
,![]() .
.
![]() 综上所述,点P的坐标为
综上所述,点P的坐标为![]() 或
或![]()
故答案是:![]() 或
或![]()

练习册系列答案
相关题目