题目内容
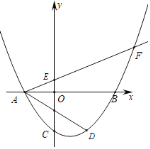
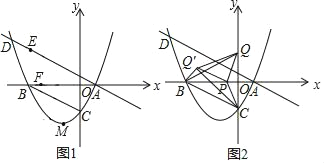
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A,B两点,交y轴于点C,连接BC.过点A作BC的平行线交抛物线于点D.
与x轴交于A,B两点,交y轴于点C,连接BC.过点A作BC的平行线交抛物线于点D.
(1)求△ABC的面积;
(2)已知点M是抛物线的顶点,在直线AD上有一动点E,x轴上有一动点F,当ME+BE最小时,求|CF﹣EF|的最大值及此时点F的坐标;
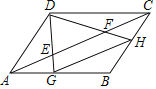
(3)如图2,在y轴正半轴上取点Q,使得CB=CQ,点P是x轴上一动点,连接PC,将△CPQ沿PC折叠至△CPQ′.连接BQ,BQ′,QQ′,当△BQQ′为等腰三角形时,直接写出点P的坐标.
【答案】(1)S△ABC=6![]() ;(2)|CF﹣EF|的最大值为2,点F的坐标为(﹣3
;(2)|CF﹣EF|的最大值为2,点F的坐标为(﹣3![]() ,0);(3)点P的坐标为(3
,0);(3)点P的坐标为(3![]() ﹣6,0),(﹣3
﹣6,0),(﹣3![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)分别将x=0和y=0代入解析式即可求出A,B,C三点的坐标,即可求出△ABC的面积;
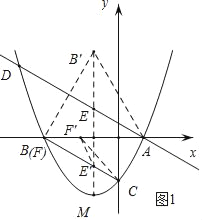
(2)先证△ABC是直角三角形,再作点B关于直线AD的对称点B',连接MB',交AD于E,则此时ME+BE有最小值,作点E关于x轴的对称点E',连接CE'并延长CE'交x轴于F,则此时|CF﹣EF|有最大值,为CE'的长度,根据点的坐标求出CE'的长度,此时点F与点B重合,即知点F坐标;
(3)分三种情况通过等边三角形,直角三角形的性质及勾股定理求出点P的坐标.
解:(1)在抛物线y=![]() 中,
中,
当y=0时,x1=﹣3![]() ,x2=
,x2=![]() ,
,
∴A(![]() ,0),B(﹣3
,0),B(﹣3![]() ,0),
,0),
当x=0时,y=﹣3,
∴C(0,﹣3),
连接AC,
∴S△ABC=![]() ABOC=6
ABOC=6![]() ;
;
(2)在Rt△ABC中,
AC=![]() =2
=2![]() ,
,
BC=![]() =6,
=6,
AB=4![]() ,
,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°,
∴tan∠ABC=![]() ,
,
∴∠ABC=30°,
如图,作点B关于直线AD的对称点B',连接MB',交AD于E,则此时ME+BE有最小值,
且∠CBB'=90°,∠ABB'=60°,
连接AB',则AB=AB',
∴△ABB'为等边三角形,
∴BB'=AB',
∴点B'在AB的垂直平分线上,
又∵M为抛物线顶点,
∴点M,B'同为抛物线对称轴上的点,
∵抛物线对称轴为x=![]() =﹣
=﹣![]() ,
,
∴xE=﹣![]() ,
,
将C(0,﹣3),B(﹣3![]() ,0)代入一次函数解析式,
,0)代入一次函数解析式,
得![]() ,
,
解得k=﹣![]() ,b=﹣3,
,b=﹣3,
∴yBC=﹣![]() x﹣3,
x﹣3,
∵BC∥AD,
∴设yAD=﹣![]() x+b,
x+b,
将A(![]() ,0)代入,
,0)代入,
得b=﹣1,
∴yAD=﹣![]() x﹣1,
x﹣1,
当xE=﹣![]() 时,yE=2,
时,yE=2,
∴E(﹣![]() ,2),
,2),
作点E关于x轴的对称点E'(﹣![]() ,﹣2),
,﹣2),
连接CE'并延长CE'交x轴于F,则此时|CF﹣EF|有最大值,为CE'的长度,
CE'=![]() =2,
=2,
理由如下:
在x轴上F外任取一点F',连接F'E',CF',
在△CE'F'中,都有|CF'﹣EE'|<CE',
∴当CE'F在一条直线上时,|CF﹣EF|有最大值,
将C(0,﹣3)E'(﹣![]() ,﹣2)代入一次函数解析式,
,﹣2)代入一次函数解析式,
得![]() ,
,
解得k=﹣![]() ,b=﹣3,
,b=﹣3,
∴yCE'=﹣![]() x﹣3,
x﹣3,
∴直线CE'与直线CB重合,
∴点F与点B重合,
∴点F的坐标为(﹣3![]() ,0),
,0),
∴|CF﹣EF|的最大值为2
CE'=![]() =2;此时点F的坐标为(﹣3
=2;此时点F的坐标为(﹣3![]() ,0);
,0);
(3)①如图2﹣1,当Q'B=Q'Q时,
由(1)知∠ABC=30°,
∴∠BCA=60°,
∵CB=CQ,
∴△CBQ为等边三角形,
∴CQ=BC=6,
又∵BQ'=QQ',
∴∠BCQ'=∠QCQ’=30°,∠CBQ'=∠CQ'B=∠CQ'Q=∠CQQ'=75°,
∴∠Q'CP=∠QCP=∠PQ'C=∠PQC=15°,
∴∠Q'PQ=60°,
∴△QQ'P是等边三角形,△BQ'P是等腰直角三角形,
设PQ=a,
则QQ'=Q'P=Q'B=a,
∴BP=![]() a,
a,
在Rt△QPO中,QP2=OP2=OQ2,
∴a2+(3![]() ﹣
﹣![]() a)2+32,
a)2+32,
解得a1=3![]() +3
+3![]() (舍去),a2=3
(舍去),a2=3![]() ﹣3
﹣3![]() ,
,
∴BP=![]() a=6
a=6![]() ﹣6,
﹣6,
∴OP=6﹣3![]() ,
,
∴P(3![]() ﹣6,0);
﹣6,0);

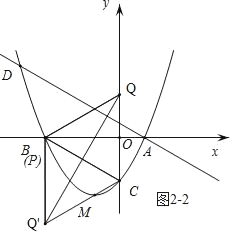
②如图2﹣2,当BQ=BQ'时,点P与点B重合,
∴P(﹣3![]() ,0);
,0);
③如图2﹣3,当QB=QQ'时,点P与点A重合,
∴P(﹣![]() ,0).
,0).

综上所述,当△BQQ′为等腰三角形时,点P的坐标为(3![]() ﹣6,0),(﹣3
﹣6,0),(﹣3![]() ,0)或(
,0)或(![]() ,0).
,0).

 名校课堂系列答案
名校课堂系列答案