题目内容
3．
三角形ABC中，AB=AC，AB的垂直平分线MN交AB，AC于D，E，若∠A=40°，则∠EBC=（ ）| A． | 15° | B． | 20° | C． | 30° | D． | 无法判断 |
分析 先根据等腰三角形的性质求出∠ABC的度数，再由线段垂直平分线的性质得出∠ABE的度数，进而可得出结论．
解答 解：∵AB=AC，∠A=40°，
∴∠ABC=$\frac{180°-40°}{2}$=70°．
∵MN是线段AB的垂直平分线，
∴AE=BE，
∴∠ABE=∠A=40°，
∴∠EBC=∠ABC-∠ABE=70°-40°=30°．
故选C．
点评 本题考查的是等腰三角形的性质，熟知等腰三角形的两个底角相等是解答此题的关键．
练习册系列答案
相关题目
13．等腰三角形一边等于5，另一边等于8，则其周长是（ ）
| A． | 18 | B． | 21 | C． | 18或21 | D． | 不能确定 |
14．
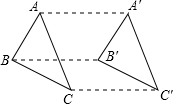如图，△ABC沿着AA′方向平移到△A′B′C′，下列说法正确的是（ ）
如图，△ABC沿着AA′方向平移到△A′B′C′，下列说法正确的是（ ）| A． | AB与A′B′平行但不相等 | B． | AB与A′B′相等但不平行 | ||
| C． | AB与A′B′平行且相等 | D． | 无法确定AB与A′B′的关系 |
15．小明用配方法解下列方程时，只有一个配方有错误，则小明配方正确的是（ ）
| A． | x2-2x-79=0化成（x-1）2=80 | B． | x2+x+9=0化成（x+4）2=25 | ||
| C． | 4t2-7t-8=0化成（t-$\frac{7}{8}$）2=$\frac{177}{64}$ | D． | 3y2-8y-2=0化成（y-$\frac{4}{3}$）2=$\frac{22}{9}$ |
12．-（+2）的相反数是（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | -$\frac{1}{2}$ | D． | -2 |
13．
如图，在△ABC中，AB=AC，∠A=70°，∠OBC=∠OCA，则∠BOC的度数为（ ）
如图，在△ABC中，AB=AC，∠A=70°，∠OBC=∠OCA，则∠BOC的度数为（ ）| A． | 140° | B． | 110° | C． | 125° | D． | 115° |