题目内容
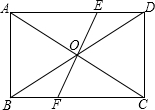 如图,在矩形ABCD中,AC、BD相交于O,EF⊥AC,AD=5,AB=3,求AE的长.
如图,在矩形ABCD中,AC、BD相交于O,EF⊥AC,AD=5,AB=3,求AE的长.考点:勾股定理,线段垂直平分线的性质,矩形的性质
专题:
分析:利用线段的垂直平分线的性质,得到EC与AE的关系,再由勾股定理计算出AE的长.
解答: 解:连接EC,由矩形的性质可得AO=CO,
解:连接EC,由矩形的性质可得AO=CO,
又因EO⊥AC,
则由线段的垂直平分线的性质可得EC=AE,
设AE=x,则ED=AD-AE=5-x,
在Rt△EDC中,根据勾股定理可得EC2=DE2+DC2,
即x2=(5-x)2+32,
解得x=3.4.
即AE=3.4.
 解:连接EC,由矩形的性质可得AO=CO,
解:连接EC,由矩形的性质可得AO=CO,又因EO⊥AC,
则由线段的垂直平分线的性质可得EC=AE,
设AE=x,则ED=AD-AE=5-x,
在Rt△EDC中,根据勾股定理可得EC2=DE2+DC2,
即x2=(5-x)2+32,
解得x=3.4.
即AE=3.4.
点评:本题考查了利用线段的垂直平分线的性质、矩形的性质及勾股定理综合解答问题的能力,此题难度一般,连接EC很关键.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
在-[-(-3)],(-1)2,-22,0,+(-
)中,负数的个数为( )
| 1 |
| 2 |
| A、2 | B、3 | C、4 | D、5 |
等腰三角形的两边长分别为5cm和10cm,则此三角形的周长( )
| A、15cm |
| B、20cm |
| C、25cm |
| D、20cm或25cm |
下列图案中,对称轴条数最多的是( )
A、 |
B、 |
C、 |
D、 |