题目内容
15.阅读下列信息:①它的图象是不经过第二象限的一条直线且与y轴的交点P到原点O的距离为3,②当x的值为2时,函数y的值为0,则y随x的增大而增大,此直线与坐标轴所围成的三角形面积为$\frac{9}{4}$.分析 设该直线的解析式为y=kx+b(k≠0),由直线不过第二象限可得出k>0、b<0,结合OP的长度可得出点P的坐标以及b的值,将点(2,0)代入函数解析式中可求出k值,进而可得出y随x的增大而增大,再根据三角形的面积公式即可求出此直线与坐标轴所围成的三角形面积.
解答 解:设该直线的解析式为y=kx+b(k≠0),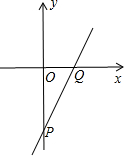
∵该直线不经过第二象限,
∴k>0,b<0.
∵该直线与y轴的交点P到原点O的距离为3,
∴点P(0,-3),b=-3.
∵当x的值为2时,函数y的值为0,
∴0=2k+b,解得:k=$\frac{3}{2}$,
∴yy随x的增大而增大.
设该直线与x轴的交点为Q,则点Q的坐标为($\frac{3}{2}$,0),
∴S△OPQ=$\frac{1}{2}$OP•OQ=$\frac{1}{2}$×$\frac{3}{2}$×3=$\frac{9}{4}$.
点评 本题考查了一次函数的性质、待定系数法求一次函数解析式以及一次函数图象与系数的关系,根据点的坐标,利用待定系数法求出函数解析式是解题的关键.

练习册系列答案
相关题目
10.如果方程2x-6=0,那么3x+8的值( )
| A. | 11 | B. | 14 | C. | 17 | D. | 20 |
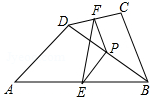 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是120°.
如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是120°.