题目内容
如图所示 在△ABC中，∠BAC的角平分线AD交D于点D．求证：| BD |
| DC |
| AB |
| AC |
考点：平行线分线段成比例
专题：证明题
分析：过B作BE∥AC，交AD的延长线交于E．由AD平分∠BAC，BE∥AC，得到∠BAD=∠E，AB=BE．再由△BDE∽△CDA，得到BE：AC=BD：DC，等线段代换即可得到AB：AC=BD：DC．
解答：证明：如图，
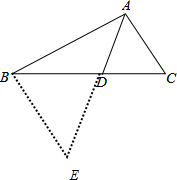
过B作BE∥AC，交AD的延长线交于E．
∵AD平分∠BAC，
∴∠BAD=∠CAD．
又∵BE∥AC，
∴∠CAD=∠E．
∴∠BAD=∠E，
∴AB=BE．
又∵BE∥AC，
∴△BDE∽△CDA，
∴BE：AC=BD：DC，
∴
=
．
过B作BE∥AC，交AD的延长线交于E．
∵AD平分∠BAC，
∴∠BAD=∠CAD．
又∵BE∥AC，
∴∠CAD=∠E．
∴∠BAD=∠E，
∴AB=BE．
又∵BE∥AC，
∴△BDE∽△CDA，
∴BE：AC=BD：DC，
∴
| BD |
| DC |
| AB |
| AC |
点评：此题考查三角形的相似的判定与性质，实际上利用三角形相似证明了角平分线定理．关键是合理添加辅助线．
练习册系列答案
相关题目
如图，AB是⊙O的直径，AC是弦，过
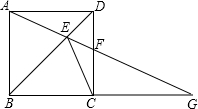如图，正方形ABCD中，点E是对角线BD上的一点，连结AE并延长，交CD于点F，交BC的延长线于点G，连结CE．
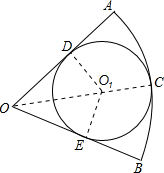如图，在扇形OAB中，⊙O1分别与