Question

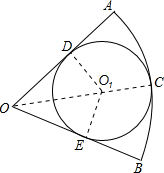如图，在扇形OAB中，⊙O₁分别与

AB

、OA、OB切于点C、D、E，∠AOB=60°，⊙O的面积为4π，若用此扇形做一个圆锥的侧面，求圆锥的底面半径．

Answer 1

考点：圆锥的计算

专题：计算题

分析：先根据圆的面积公式得到O₁D=2，再利用两圆相切的性质与切线的性质得到OC=OO₁+O₁C=OO₁+2，O₁D⊥OA，O₁E⊥OB，则根据角平分线的判定定理得到∠AOC=30°，在Rt△OO₁D中利用含30度的直角三角形三边的关系可得OC=6，然后根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长和弧长公式求解．

解答：解：∵⊙O的面积为4π，
∴πO₁D²=4π，解得O₁D=2，
∵⊙O₁分别与

AB

、OA、OB切于点C、D、E，
∴OC=OO₁+O₁C=OO₁+2，O₁D⊥OA，O₁E⊥OB，
∴∠AOC=∠BOC=

1

2

∠AOB=30°，
在Rt△OO₁D中，∵O₁D=2，∠DOO₁=30°，
∴OO₁=2O₁D=4，
∴OC=6，
设圆锥的底面半径为r，
则2πr=

60•π•6

180

，即得r=1，
即圆锥的底面半径为1．

点评：本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆的母线长．也考查了两圆相切的性质与切线的性质．