题目内容
 如图,点E在?ABCD的边BC延长线上,连AE,交边CD于点F.在不添加辅助线的情况下,图中相似三角形有( )
如图,点E在?ABCD的边BC延长线上,连AE,交边CD于点F.在不添加辅助线的情况下,图中相似三角形有( )| A、1对 | B、2对 | C、3对 | D、4对 |
考点:相似三角形的判定,平行四边形的性质
专题:
分析:根据平行四边形的性质及相似三角形的判定方法进行分析即可.
解答:解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴△AFD∽△EFC∽△EAB.
故选C.
∴AD∥BC,AB∥CD,
∴△AFD∽△EFC∽△EAB.
故选C.
点评:此题考查了相似三角形的判定:
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.

练习册系列答案
相关题目
已知甲、乙两坡的倾斜角分别为α、β,若甲坡比乙坡陡,则下列选项成立的是( )
| A、cosα<cosβ |
| B、cosα>cosβ |
| C、sinα<sinβ |
| D、tanα<tanβ |
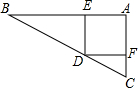 如图,一个直角三角形的苗圃由正方形花坛和两块直角三角形的草皮组成,两个直角三角形的斜边长分别为3m和6m.
如图,一个直角三角形的苗圃由正方形花坛和两块直角三角形的草皮组成,两个直角三角形的斜边长分别为3m和6m. 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB交AB于D,已知cos∠ACD=
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB交AB于D,已知cos∠ACD= 如图,在△ABC中,BC=2.点A的坐标是(-4,3),点B的坐标是(-3,1).
如图,在△ABC中,BC=2.点A的坐标是(-4,3),点B的坐标是(-3,1).