题目内容
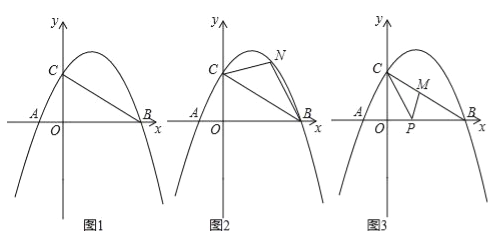
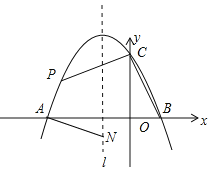
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其对称轴1为
,其对称轴1为![]() .
.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点![]() 在第二象限内的抛物线上,动点
在第二象限内的抛物线上,动点![]() 在对称轴1上.
在对称轴1上.
①当![]() ,且
,且![]() 时,求此时点
时,求此时点![]() 的坐标;
的坐标;
②当四边形![]() 的面积最大时,求四边形
的面积最大时,求四边形![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
【答案】(1)y=﹣x2﹣2x+3,顶点为(﹣1,4);(2)①![]() ;②
;②![]() ,
,![]() .
.
【解析】
(1)把点A、B、C的坐标代入二次函数表达式,即可求解;
(2)①由PA⊥NA,且PA=NA,可证△PAD≌△ANQ(AAS),则PD=AQ,PD=AQ=AO-QO=3-1=2,即:即y=-x2-2x+3=2,即可求解;
②利用S四边形PABC=S△OBC+S△CPO+S△POA,求解即可.
解:(1)把点A、B、C的坐标代入二次函数表达式得: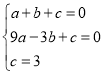 ,解得
,解得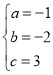 ,
,
故:抛物线的解析式为y=﹣x2﹣2x+3,
∴顶点坐标为(﹣1,4);
(2)∵A(﹣3,0),B(1,0),
OA=3,OB=1,
如解图,作PD⊥x轴于点D,设对称轴l与x轴交于点Q,连接AC,OP,
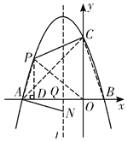
①∵点P在y=﹣x2﹣2x+3上,
∴设点P(x,﹣x2﹣2x+3),
∵PA⊥NA,且PA=NA,
∴∠PAD+∠APD=∠PAD+∠NAQ=90°,
∴∠APD=∠NAQ,
又∵∠PDA=∠AQN=90°,
∴△PAD≌△ANQ(AAS),
∴PD=AQ,
∴PD=AQ=AO﹣QO=3﹣1=2
即:y=﹣x2﹣2x+3=2
解得:![]() (舍去)或
(舍去)或![]()
∴点P坐标为![]() ;
;
②连接OP,设P(x,﹣x2﹣2x+3),且﹣3<x<0
S四边形PABC=S△OBC+S△CPO+S△POA
∵![]() ,
,![]()
又﹣3<x<0,所以![]() ,
,
![]()
∴S四边形PABC=S△OBC+S△CPO+S△POA
![]() ,
,
∴当![]() 时,S四边形PABC最大为
时,S四边形PABC最大为![]() ,
,
此时![]() .
.

练习册系列答案
相关题目