题目内容
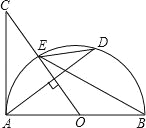
【题目】如图，Rt△ABC，∠B=90°，∠C=30°，O为AC上一点，OA=2，以O为圆心，以OA为半径的圆与CB相切于点E，与AB相交于点F，连接OE、OF，则图中阴影部分的面积是_______．
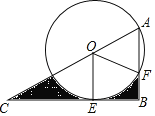
【答案】
π
【解析】
根据扇形面积公式以及三角形面积公式即可求出答案．
∵∠B=90°，∠C=30°，
∴∠A=60°，
∵OA=OF，
∴△AOF是等边三角形，
∴∠COF=120°，
∵OA=2，
∴扇形OGF的面积为：
=
∵OA为半径的圆与CB相切于点E，
∴∠OEC=90°，
∴OC=2OE=4，
∴AC=OC+OA=6，
∴AB=
AC=3，
∴由勾股定理可知：BC=3
∴△ABC的面积为：×3×3=
∵△OAF的面积为：×2×=，
∴阴影部分面积为：
﹣﹣
π=
﹣
π
故答案为：﹣π.
练习册系列答案
名校课堂系列答案
相关题目
