题目内容
14.先化简,再求值:$\frac{{x}^{2}+2x}{1+x}$÷(x2+$\frac{{x}^{2}}{x+1}$),其中x=$\sqrt{2}$.分析 把分式的分子分母分解因式,首先计算括号内的式子,然后转化为乘法即可化简,然后代入x的值计算即可.
解答 解:原式=$\frac{x(x+2)}{x+1}$÷$\frac{{x}^{2}(x+1)+{x}^{2}}{x+1}$
=$\frac{x(x+2)}{x+1}$•$\frac{x+1}{{x}^{2}(x+2)}$
=$\frac{1}{x}$.
当x=$\sqrt{2}$时,原式=$\frac{\sqrt{2}}{2}$.
点评 本题综合考查了分式的化简求值,分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.

练习册系列答案
相关题目
3.把x=22000输入如图所示的运算系统,则第2010次输出的值是( )


| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
4.在①正三角形,②正方形,③正五边形,④正六边形,⑤圆,这五种几何图形中,既是轴对称,又是中心对称图形的是( )
| A. | ①②④⑤ | B. | ②③④⑤ | C. | ②④⑤ | D. | ①③⑤ |
 如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.
如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.
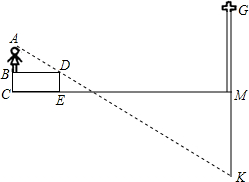 在一次测量活动中,同学们想测量一条河的宽度,如图,他们选取了河岸上距离河岸边D处3m的B点作为观测点,此时身高AB=1.5m的小敏站在B处,恰好能看见河正对岸边上的电线杆GM在水中的全部倒影MK,若河岸高出水面的高度DE为0.75m,电线杆高为4.5m,求河宽EM.
在一次测量活动中,同学们想测量一条河的宽度,如图,他们选取了河岸上距离河岸边D处3m的B点作为观测点,此时身高AB=1.5m的小敏站在B处,恰好能看见河正对岸边上的电线杆GM在水中的全部倒影MK,若河岸高出水面的高度DE为0.75m,电线杆高为4.5m,求河宽EM.