题目内容
 如图,CA⊥AB于点A,DB⊥AB于点B,AB=12m,AC=4m.一只蚂蚁由点B向点A爬行,每分钟爬行1m,另一只蚂蚁由点B向点D爬行,每分钟爬行2m.它们同时出发,点P,Q为它们在某一时刻的位置,爬行几分钟后,以A,C,P为顶点的三角形与以B,P,Q为顶点的三角形相似?并说明理由.
如图,CA⊥AB于点A,DB⊥AB于点B,AB=12m,AC=4m.一只蚂蚁由点B向点A爬行,每分钟爬行1m,另一只蚂蚁由点B向点D爬行,每分钟爬行2m.它们同时出发,点P,Q为它们在某一时刻的位置,爬行几分钟后,以A,C,P为顶点的三角形与以B,P,Q为顶点的三角形相似?并说明理由.考点:相似三角形的应用
专题:
分析:分类讨论:△ACP∽△BPQ和△ACP∽△BQP两种情况.利用相似三角形的对应边成比例来求t的值.
解答:解:设爬行t分钟后,以A,C,P为顶点的三角形与以B,P,Q为顶点的三角形相似.
①当△ACP∽△BPQ时,
=
,即
=
,
解得t=4(不合题意,舍去);
②当△ACP∽△BQP时,
=
,即
=
,
解得t=10.
综上所述,当t=10时,以A、P、M为顶点的三角形与以B,P,Q为顶点的三角形相似.
①当△ACP∽△BPQ时,
| AC |
| AP |
| BP |
| BQ |
| 4 |
| 12-t |
| t |
| 2t |
解得t=4(不合题意,舍去);
②当△ACP∽△BQP时,
| AC |
| AP |
| BQ |
| BP |
| 4 |
| 12-t |
| 2t |
| t |
解得t=10.
综上所述,当t=10时,以A、P、M为顶点的三角形与以B,P,Q为顶点的三角形相似.
点评:考查了相似三角形的应用,解答时,一定要分类讨论,以防漏解.另外,利用相似三角形的对应边成比例解题时,务必找准对应边.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 如图,在△ABC中,BD=2DC,CE=2EA,AD与BE交于点F,且△ABC的面积为42,则△AEF的面积是多少?
如图,在△ABC中,BD=2DC,CE=2EA,AD与BE交于点F,且△ABC的面积为42,则△AEF的面积是多少?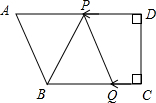 如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q三点为顶点的三角形为等腰三角形?
如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q三点为顶点的三角形为等腰三角形?
 如图是由小立方体组成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,请画出相应的主视图和左视图.
如图是由小立方体组成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,请画出相应的主视图和左视图.