不等式组$\left\{\begin{array}{l}{2x-3＜5}\\{3x+2≥-1}\end{array}\right.$的解集是( )A．x＜4B．x≥-1C．-1≤x＜4D．x≥4或x＜-1 题目和参考答案——青夏教育精英家教网—

题目内容

1．不等式组$\left\{\begin{array}{l}{2x-3＜5}\\{3x+2≥-1}\end{array}\right.$的解集是（　　）

A．

x＜4

B．

x≥-1

C．

-1≤x＜4

D．

x≥4或x＜-1

分析先求出两个不等式的解集，再求其公共解．

解答解：$\left\{\begin{array}{l}{2x-3＜5①}\\{3x+2≥-1②}\end{array}\right.$，
由①得x＜4，
由②得x≥-1，
所以不等式组的解集是-1≤x＜4．
故选C．

点评本题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解．求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．

练习册系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

赢在起跑线天天100分小学优化测试卷系列答案

5．计算：30×$（\frac{1}{2}-\frac{2}{3}+0.4）$，应运用（　　）

9．2cos30°+$（-\frac{1}{2}）^{0}$×（-1）²⁰¹³=$\sqrt{3}$-1．

16．若x=0是方程（m-2）x²+5x+m²-2m=0的根，则m的值为（　　）

6．在直角坐标系中作出函数y=2x-5的图象，观察图象．
（1）回答：x取何值时，2x-5=0？x在何范围取值时，2x-5＞-5？
（2）如果函数y=2x-5的图象与x轴交于A点，与平行于x轴的直线l交于B点，连接OB，若△BOA的面积等于5，求点B的坐标．

13．

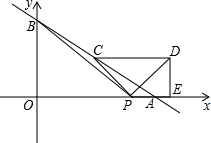如图所示，直线y=-$\frac{3}{4}$x+6与x、y轴分别交于A点、B点，C点是AB的中点，点P从A出发以每秒1个单位的速度沿射线AO方向运动，将点C绕P点顺时针旋转90°得到点D，作DE⊥x轴，垂足为E，连接PC，PD，PB．设点P的运动时间为t秒（0＜t＜8），当以P，D，E为顶点的三角形与△BOP相似时，写出所有t的值0或$\frac{16}{3}$或6-$\sqrt{22}$．

11．

某校测量了七（1）班学生的身高（精确到1cm），得到如图所示的频数分布直方图（每组含最小值，不含最大值），根据图中信息，计算出该班学生的平均身高大约是162cm．

试题分类