题目内容
13.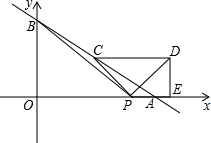 如图所示,直线y=-$\frac{3}{4}$x+6与x、y轴分别交于A点、B点,C点是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P点顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0<t<8),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值0或$\frac{16}{3}$或6-$\sqrt{22}$.
如图所示,直线y=-$\frac{3}{4}$x+6与x、y轴分别交于A点、B点,C点是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P点顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0<t<8),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值0或$\frac{16}{3}$或6-$\sqrt{22}$.
分析 过C作CF⊥x轴于F,先求得CF=3,然后根据△PFC≌△DEP求得PE=CF=3,PE=4-t,OP=8-t或OP=t-8,最后根据以P,D,E为顶点的三角形与△BOP相似时,对应边成比例即可求得t的值.
解答 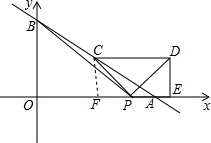 解:过C作CF⊥x轴于F,
解:过C作CF⊥x轴于F,
∵直线y=-$\frac{3}{4}$x+6与x、y轴分别交于A点、B点,
∴A(8,0),B(0,6),
∴OA=8,OB=6,
∵∠AOB=∠PFC,
∴CF∥OB,
∵AC=BC,
∴FC=$\frac{1}{2}$OB=3,FA=$\frac{1}{2}$OA=4,
∴PF=4-t,
∵∠FPC+∠DPE=90°,∠FPC+∠PCF=90°,
∴∠PCF=∠DPE,
∵PC=PD,∠PFC=∠PED=90°,
∴△PFC≌△DEP,
∴DE=PF=4-t,PE=FC=3,
∵以P,D,E为顶点的三角形与△BOP相似时,
∴$\frac{PE}{OP}$=$\frac{DE}{OB}$或$\frac{PE}{OB}$=$\frac{DE}{OP}$即$\frac{3}{8-t}$=$\frac{4-t}{6}$或$\frac{3}{6}$=$\frac{4-t}{8-t}$,
解得:t=6+$\sqrt{22}$或t=6-$\sqrt{22}$或t=0或t=$\frac{16}{3}$.
∵0<t<8,
故答案为:0或$\frac{16}{3}$或6-$\sqrt{22}$.
点评 本题是一次函数综合题型,主要考查了利用一次函数与坐标轴的交点根据相似三角形对应边成比例求得移动点移动的距离,难点在于要把各种情况考虑周全.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
1.不等式组$\left\{\begin{array}{l}{2x-3<5}\\{3x+2≥-1}\end{array}\right.$的解集是( )
| A. | x<4 | B. | x≥-1 | C. | -1≤x<4 | D. | x≥4或x<-1 |
5.将多项式x2+4加上一个整式,使它成为完全平方式,能满足上述条件的整式是( )
| A. | 8x | B. | -4x | C. | 2x | D. | -2x |
3.在+(-2),-(-$\frac{1}{2}$),-[+(-2)],+[-(+$\frac{1}{2}$)],+[-(-2)]中,负数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个或3个以上 |