题目内容
8.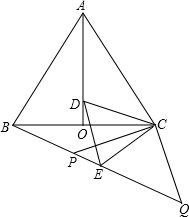 如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.(1)求证:△ACD≌△BCE.
(2)求∠QBC的度数?
(3)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=13,若BC=24时,求PQ的长.
分析 (1)由等边三角形的性质可知AC=BC,CD=CE.∠ACB=∠DCE=60°,从而得到∠ACD=∠BCE,依据SAS可证明△ACD≌△BCE;
(2)由角平分线的定义可知:∠CAD=$\frac{1}{2}$∠BAC=30°,由全等三角形的性质可知∠CBE=∠CAD=30°,故此∠QBC=30°;
(3)在△BCH中根据30°所对的直角边是斜边的一半可知HC=12,由等腰三角形三线合一的性质可知PH=HQ,然后在Rt△PCH中由勾股定理可求得PH=5,从而得到PQ=10.
解答 (1)证明:∵△ABC和△CDE为等边三角形,
∴AC=BC,CD=CE.∠ACB=∠DCE=60°.
∴∠ACB-∠DCO=∠DCE-∠DCO.
∴∠ACD=∠BCE.
在△ACD和△BCE中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS).
(2)∵△ABC为等边三角形且AO是∠BAC的角平分线,
∴∠CAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×60°=30°.
∵△ACD≌△BCE,
∴∠CBE=∠CAD=30°.
∴∠QBC=30°.
(3)过点C作CH⊥BQ于H.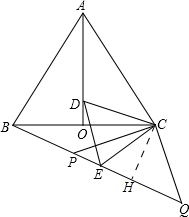
∵∠QBC=30°,∠CHB=90°,
∴CH=$\frac{1}{2}$BC=$\frac{1}{2}$×24=12.
∵PC=CQ=13,CH⊥PQ,
∴PH=QH.
∵在Rt△PCH中,PH=$\sqrt{P{C}^{2}-H{C}^{2}}$=5.
∴PH=QH=5.
∴PQ=10.
点评 本题主要考查的是等边三角形的性质、全等三角形的性质和判定、勾股定理的应用、等腰三角形的性质、含30°直角三角形的性质,证得∠QBC=30°是解题的关键.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | 三角形的内角和等于180度 | |
| B. | 三角形两边之和大于第三边 | |
| C. | 三角形的面积等于一条边的长与该边上的高的积 | |
| D. | 三角形中可以有两个内角是钝角 |
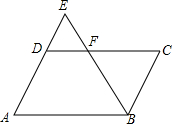 如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论正确的有( )
如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论正确的有( )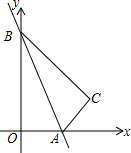 如图,一次函数的图象与x轴,y轴分别相交于A、B,将△AOB沿直线AB翻折,得△ACB,若C($\frac{3}{2}$,$\frac{{\sqrt{3}}}{2}$),则:
如图,一次函数的图象与x轴,y轴分别相交于A、B,将△AOB沿直线AB翻折,得△ACB,若C($\frac{3}{2}$,$\frac{{\sqrt{3}}}{2}$),则: