Question

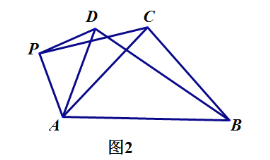
【题目】已知：AB为⊙O的直径，点C，D在⊙O上，连接AD，OC．

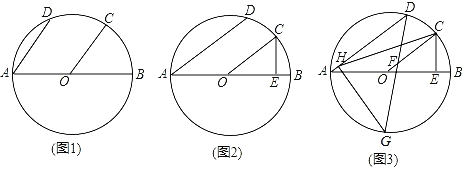
（1）如图1，求证：AD∥OC；

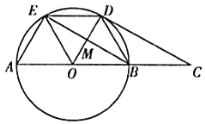
（2）如图2，过点C作CE⊥AB于点E，求证：AD＝2OE；

（3）如图3，在（2）的条件下，点F在OC上，且OF＝BE，连接DF并延长交⊙O于点G，过点G作CH⊥AD于点H，连接CH，若∠CFG＝135°，CE＝3，求CH的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）

【解析】

（1）如图1（见解析），先根据圆心角定理得出，从而可得，再根据圆周角定理可得，从而可得，然后根据平行线的判定即可得证；

（2）如图2（见解析），先根据圆周角定理得出，再根据题（1）的结论、直角三角形的性质得出，然后根据圆周角定理、圆心角定理可得，最后根据垂径定理、中位线定理得出，由此即可得证；

（3）如图3（见解析），先根据圆周角定理、平行线的性质得出，再根据垂径定理可得，然后根据三角形全等的判定定理与性质得出，从而可得，在中，利用勾股定理可得，又根据直角三角形的性质、矩形的性质、圆的相交弦定理得出，，从而可得，最后利用勾股定理即可得．

（1）如图1，连接OD

∵

∴

由圆周角定理得：

∴

∴；

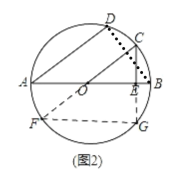
（2）如图2，延长CO交圆O于F，延长CE交圆O于G，连接FG，BD

则

∵于E

∴，

∴

∵，

∴

∴

∵，

OE是的中位线

∴

∴，即；

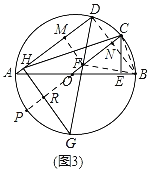
（3）如图3，延长CO交圆O于P，连接BD交OC于N，作PM⊥AD于M，连接BC、BF，则

∵

∴

∴

∵于E

∴

∵，

∴

∴

∴

∵

∴

∴，

设，则

在中，，即，解得

∴

∵

∴

∵

∴

∴

设CP交HG于R

∵

∴

∴

∴，，

又∵，即

解得

∴

在中，．