题目内容
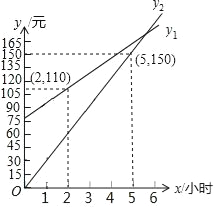
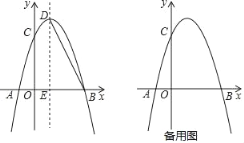
【题目】如图,点![]() ,过点
,过点![]() 做直线
做直线![]() 平行于
平行于![]() 轴,点
轴,点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)点![]() 在直线
在直线![]() 上,且位于
上,且位于![]() 轴的上方,将
轴的上方,将![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 恰好落在直线
恰好落在直线![]() 上,求点
上,求点![]() 的坐标和直线
的坐标和直线![]() 的解析式;
的解析式;
(3)设点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,当
上,当![]() 为等边三角形时,求点
为等边三角形时,求点![]() 的坐标.
的坐标.
【答案】(1)(3,0);(2)A(1,![]() );直线BD为
);直线BD为![]() ;(3)点P的坐标为(
;(3)点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)根据题意,点B、C关于点M对称,即可求出点C的坐标;
(2)由折叠的性质,得AB=CB,BD=AD,根据勾股定理先求出AM的长度,设点D为(1,a),利用勾股定理构造方程,即可求出点D坐标,然后利用待定系数法求直线BD.
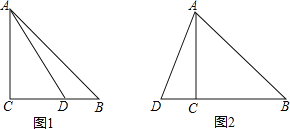
(3)分两种情形:如图2中,当点P在第一象限时,连接BQ,PA.证明点P在AC的垂直平分线上,构建方程组求出交点坐标即可.如图3中,当点P在第三象限时,同法可得△CAQ≌△CBP,可得∠CAQ=∠CBP=30°,构建方程组解决问题即可.
解:(1)根据题意,
∵点B、C关于点M对称,且点B、M、C都在x轴上,
又点B(![]() ),点M(1,0),
),点M(1,0),
∴点C为(3,0);
(2)如图:

由折叠的性质,得:AB=CB=4,AD=CD=BD,
∵BM=2,∠AMB=90°,
∴![]() ,
,
∴点A的坐标为:(1,![]() );
);
设点D为(1,a),则DM=a,BD=AD=![]() ,
,
在Rt△BDM中,由勾股定理,得
![]() ,
,
解得:![]() ,
,
∴点D的坐标为:(1,![]() );
);
设直线BD为![]() ,则
,则
 ,解得:
,解得: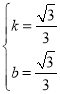 ,
,
∴直线BD为:![]() ;
;
(3)如图2中,当点P在第一象限时,连接BQ,PA.
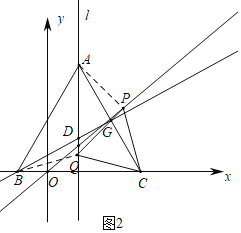
∵△ABC,△CPQ都是等边三角形,
∴∠ACB=∠PCQ=60°,
∴∠ACP=∠BCQ,
∵CA=CB,CP=CQ,
∴△ACP≌△BCQ(SAS),
∴AP=BQ,
∵AD垂直平分线段BC,
∴QC=QB,
∴PA=PC,
∴点P在AC的垂直平分线上,
由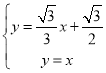 ,解得
,解得 ,
,
∴P(![]() ,
,![]() ).
).
如图3中,当点P在第三象限时,同法可得△CAQ≌△CBP,
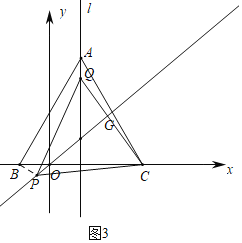
∴∠CAQ=∠CBP=30°,
∵B(-1,0),
∴直线PB的解析式为![]() ,
,
由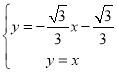 ,解得:
,解得: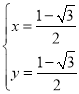 ,
,
∴P(![]() ,
,![]() ).
).