题目内容
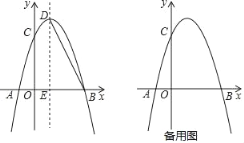
【题目】如图，抛物线y=﹣
x2+bx+c与x轴交于点A和点B，与y轴交于点C，点B坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点，过点D作x轴的垂线，垂足为E，连接BD．
（1）求抛物线的解析式及点D的坐标；
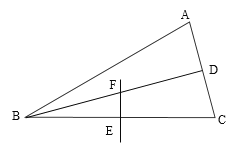
（2）点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；
（3）若点P是x轴上方抛物线上的动点，以PB为边作正方形PBFG，随着点P的运动，正方形的大小、位置也随着改变，当顶点F或G恰好落在y轴上时，请直接写出点P的横坐标．
【答案】（1）D（2，8）；（2）（﹣1，
）或（﹣3，﹣
）；（3）点P的横坐标为1+
或4或0．
【解析】
（1）由B、C的坐标，利用待定系数法可求得抛物线解析式，再求其顶点D即可；
（2）过F作FG⊥x轴于点G，可设出F点坐标，利用△FBG∽△BDE，由相似三角形的性质可得到关于F点坐标的方程，可求得F点的坐标；
（3）设P（m，
m2+2m+6），有四种情况：
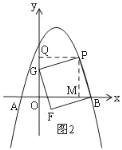
①如图2，当G在y轴上时，过P作PQ⊥y轴于Q，作PM⊥x轴于M，
证明△PQG≌△PMB，则PQ=PM，列方程可得m的值；
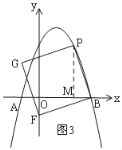
②当F在y轴上时，如图3，过P作PM⊥x轴于M，同理得结论；
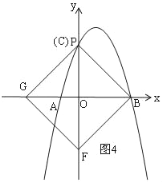
③当F在y轴上时，如图4，此时P与C重合；
④当G在y轴上时，如图5，过P作PM⊥x轴于M，作PN⊥y轴于N，列方程可得m的值．
解：（1）把点B坐标为（6，0），点C坐标为（0，6）代入抛物线y=﹣
x2+bx+c得：
，
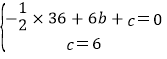解得：
，
∴y=﹣x2+2x+6=﹣（x﹣2）2+8，
∴D（2，8）；
（2）如图1，过F作FG⊥x轴于点G，
设F（x，﹣x2+2x+6），则FG=|﹣x2+2x+6|，
∵∠FBA=∠BDE，∠FGB=∠BED=90°，
∴△FBG∽△BDE，
∴
，
∵B（6，0），D（2，8），
∴E（2，0），BE=4，DE=8，OB=6，
∴BG=6﹣x，
∴
＝
＝ ，
当点F在x轴上方时，有6﹣x=2（﹣+2x+6），
解得x=﹣1或x=6（舍去），
此时F点的坐标为（﹣1，
）；
当点F在x轴下方时，有6﹣x=2（－2x－6），
解得x=﹣3或x=6（舍去），
此时F点的坐标为（﹣3，﹣
）；
综上可知F点的坐标为（﹣1，）或（﹣3，﹣ ）；
（3）设P（m，
），
有三种情况：
①如图2，当G在y轴上时，过P作PQ⊥y轴于Q，作PM⊥x轴于M，
∵四边形PBFG是正方形，
∴PG=PB，
∵∠PQG=∠PMB=90°，∠QPG=∠MPB，
∴△PQG≌△PMB，
∴PQ=PM，
即m=﹣ m2+2m+6，
解得：m1=1+，m2=1﹣（舍），
∴P的横坐标为1+，
②当F在y轴上时，如图3，过P作PM⊥x轴于M，
同理得：△PMB≌△BOF，
∴OB=PM=6，
即﹣m2+2m+6=6，
m1=0（舍），m2=4，
∴P的横坐标为4，
③当F在y轴上时，如图4，此时P与C重合，
此时P的横坐标为0，
综上所述，点P的横坐标为1+ 或4或0．
