Question

【题目】对于平面直角坐标系xOy中的和点P，给出如下定义：如果在上存在一个动点Q，使得是以CQ为底的等腰三角形，且满足底角，那么就称点P为的“关联点”．

当的半径为2时，

在点，，中，的“关联点”是______；

如果点P在射线上，且P是的“关联点”，求点P的横坐标m的取值范围．

的圆心C在x轴上，半径为4，直线与两坐标轴交于A和B，如果线段AB上的点都是的“关联点”，直接写出圆心C的横坐标n的取值范围．

Answer 1

【答案】（1）①和；②；（2）或．

【解析】

（1）①由题意可知：⊙O的“关联点”在以O为圆心半径分别为1和2的圆环内部包括大圆上的点，不包括小圆上的点，由此即可判断；

②由题意可知：⊙O的“关联点”在以O为圆心半径分别为1和2的圆环内部包括大圆上的点，不包括小圆上的点，射线与该圆环交于点P和，由题意易知，，由此即可判断；

（2）求出四个特殊位置的点C的坐标即可判断；

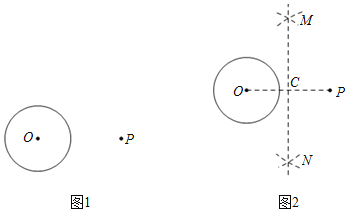
解：如图1中，

由题意可知：的“关联点”在以O为圆心半径分别为1和2的圆环内部包括大圆上的点，不包括小圆上的点，

在点，，中，的“关联点”是和．

故答案为和．

如图2中，

由题意可知：的“关联点”在以O为圆心半径分别为1和2的圆环内部包括大圆上的点，不包括小圆上的点，

射线与该圆环交于点P和，

由题意易知，，

．

如图3中，

当时，，此时，

当时，此时，

当时，线段AB上的点都是的“关联点”，

当点到直线AB的距离为2时，易知，

当时，，

当时，线段AB上的点都是的“关联点”，

综上所述，满足条件的n的值的范围为：或．

故答案为：（1）①和；②；（2）或．