题目内容
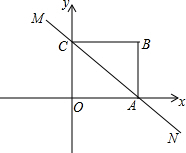
 如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.(1)求直线MN的函数关系式;
(2)点P从O出发,以每秒1个单位的速度沿x的正半轴匀速运动,运动时间为t,△ABP面积为S,求S与t的函数关系;
(3)在(2)的条件下,当t=4秒时,在平面内是否存在一点Q,使得以A,C,P,Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)利用待定系数法即可求得直线的解析式;
(2)分P在线段OA上和在线段OA的延长线上时,两种情况进行讨论,利用三角形的面积公式求解;
(3)分平行四边形ACQP,平行四边形APCQ和平行四边形PQAC三种情况进行讨论,根据平行四边形的性质即可求解.
(2)分P在线段OA上和在线段OA的延长线上时,两种情况进行讨论,利用三角形的面积公式求解;
(3)分平行四边形ACQP,平行四边形APCQ和平行四边形PQAC三种情况进行讨论,根据平行四边形的性质即可求解.
解答:解:(1)解方程x2-14x+48=0得:x1=6,x2=8,
则OA=8,OC=6,A的坐标是(8,0),C的坐标是(0,6).
设直线MN的解析式是y=kx+b,
根据题意得:
,
解得:
,
则直线MN的解析式是:y=-
x+6;
(2)当P在线段OA上时,即0≤t≤8时,AP=8-t,
则S=
×(8-t)×6=24-3t,
当t>8时,AP=t-8,则S=
×(t-8)×6=3t-24;
(3)当t=4秒时,P的坐标是(4,0),
则当是平行四边形ACQP时,CQ∥x轴,且CQ=AP=4,则Q的坐标是(-4,6);
当是平行四边形APCQ时,CQ∥AP且CQ=AP,则Q的坐标是(4,6);
当是平行四边形PQAC时,AP的中点是(6,0),Q的纵坐标是-6,设横坐标是m,则
=6,
解得:m=12,
则Q的坐标是(12,-6).
则OA=8,OC=6,A的坐标是(8,0),C的坐标是(0,6).
设直线MN的解析式是y=kx+b,
根据题意得:
|
解得:
|

则直线MN的解析式是:y=-
| 3 |
| 4 |
(2)当P在线段OA上时,即0≤t≤8时,AP=8-t,
则S=
| 1 |
| 2 |
当t>8时,AP=t-8,则S=
| 1 |
| 2 |
(3)当t=4秒时,P的坐标是(4,0),
则当是平行四边形ACQP时,CQ∥x轴,且CQ=AP=4,则Q的坐标是(-4,6);
当是平行四边形APCQ时,CQ∥AP且CQ=AP,则Q的坐标是(4,6);
当是平行四边形PQAC时,AP的中点是(6,0),Q的纵坐标是-6,设横坐标是m,则
| m |
| 2 |
解得:m=12,
则Q的坐标是(12,-6).
点评:本题考查了待定系数法求函数的解析式,以及平行四边形的判定,正确对以A,C,P,Q为顶点的四边形是平行四边形进行讨论是关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
下列分解因式错误的是( )
| A、x2-2xy+y2=(x-y)2 |
| B、x3-x2+x=x(x2-x) |
| C、x2y-xy2=xy(x-y) |
| D、x2-y2=(x-y)(x+y) |
 如图,已知在?ABCD中,点E、F是对角线AC上的任意两点,且AE=CF.求证:△ADE≌△CBF.
如图,已知在?ABCD中,点E、F是对角线AC上的任意两点,且AE=CF.求证:△ADE≌△CBF.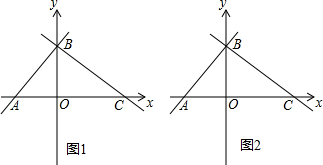
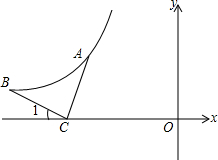 如图,反比例函数y=
如图,反比例函数y= 在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(提示:连接DB)单位:厘米.
在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(提示:连接DB)单位:厘米. 已知在平行四边形ABCD中,E、F分别是边AB、AD上的点,EF与对角线AC交于点P,若
已知在平行四边形ABCD中,E、F分别是边AB、AD上的点,EF与对角线AC交于点P,若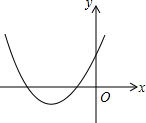 已知二次函数y=ax2+bx+c的图象如图所示,则
已知二次函数y=ax2+bx+c的图象如图所示,则