题目内容
如图,直线y=x+4与x轴、y轴分别交于A、B两点,直线y=-x+b过点B且与x轴交于点C.
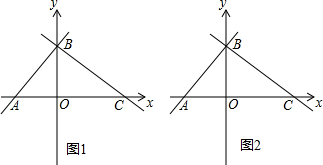
(1)求直线BC的表达式;
(2)若动点P从点C出发沿CA方向向点A运动点P不与点A、C重合,同时动点Q从点A出发沿折线AD-BC向点C运动,(点Q不与点A、C重合)动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒
个单位长度,当其中一个动点达到终点时,另一个动点也随之停止运动.设△CPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式,并写出自变量t的取值范围.

(1)求直线BC的表达式;
(2)若动点P从点C出发沿CA方向向点A运动点P不与点A、C重合,同时动点Q从点A出发沿折线AD-BC向点C运动,(点Q不与点A、C重合)动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒
| 2 |
考点:一次函数综合题
专题:
分析:(1)根据待定系数法即可求得;
(2)分两种情况讨论即可求得;当P点在CO之间运动时,作QH⊥x轴,根据
=
,求得QH=
t,然后根据三角形的面积公式即可求得;当P在AO之间运动时,根据
=
,求得QH=8-
t,然后根据三角形的面积公式即可求得.
(2)分两种情况讨论即可求得;当P点在CO之间运动时,作QH⊥x轴,根据
| QH |
| OB |
| AQ |
| AB |
| 2 |
| QH |
| OB |
| CQ |
| BC |
| 2 |
解答:解:(1)∵直线y=x+4与x轴、y轴分别交于A、B两点,
∴A点坐标(-4﹐0),B点坐标(0﹐4﹚,
∵直线y=-x+b过点B,
∴b=4,
∴直线BC的表达式y=-x+4;
﹙2﹚∵直线BC的表达式y=-x+4,
∴C(4,0),
∴OA=OB=OC=4,
∴AB=BC=4
,
如图1,当P点在CO之间运动时,作QH⊥x轴.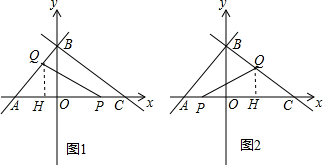
∵
=
,
∴
=
,
∴QH=
t
∴S△CPQ=
CP•QH=
•t•
t=
t2﹙0<t≤4﹚,
如图2,当P在AO之间运动时,
∵
=
,
∴
=
,
∴QH=8-
t,
∴S△CPQ=
t•﹙8-
t)=-
t2+4t﹙4≤t<8﹚.
∴A点坐标(-4﹐0),B点坐标(0﹐4﹚,
∵直线y=-x+b过点B,
∴b=4,
∴直线BC的表达式y=-x+4;
﹙2﹚∵直线BC的表达式y=-x+4,
∴C(4,0),
∴OA=OB=OC=4,
∴AB=BC=4
| 2 |
如图1,当P点在CO之间运动时,作QH⊥x轴.

∵
| QH |
| OB |
| AQ |
| AB |
∴
| QH |
| 4 |
| 2t | ||
4
|
∴QH=
| 2 |
∴S△CPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
如图2,当P在AO之间运动时,
∵
| QH |
| OB |
| CQ |
| BC |
∴
| QH |
| 4 |
8
| ||
4
|
∴QH=8-
| 2 |
∴S△CPQ=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
点评:本题是一次函数的综合题,考查了直线与坐标轴的交点,待定系数法求解析式,三角形的面积等,重点是(2),注意分别讨论,不要漏解.

练习册系列答案
相关题目
 如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根. 如图,C是
如图,C是