题目内容
10. △ABC中,∠BAC=90°,AB=AC,BD=3,CE=4,AD=3DE,求△ABD的面积.
△ABC中,∠BAC=90°,AB=AC,BD=3,CE=4,AD=3DE,求△ABD的面积.
分析 以A为圆心,以AD长为半径画弧,交BC于G,连接AG,则AG=AD=3DE;作AF⊥BC,根据等腰三角形三线合一的性质得出BF=FC,根据已知求得DF=FG=FE+1=$\frac{1}{2}$(DE+1).BF=3+DF=3+$\frac{1}{2}$(DE+1)=$\frac{1}{2}$(DE+7),进而得出AF2=AD2-DF2=$\frac{1}{4}$(35DE2-2DE-1),BF2=$\frac{1}{4}$(DE2+14DE+49),根据直角三角形斜边中线的性质得出BF=CF,得出$\frac{1}{4}$(35DE2-2DE-1)=$\frac{1}{4}$(DE2+14DE+49),解得DE=$\frac{25}{17}$,进而求得BC,进一步求得AF,然后根据三角形面积公式求得即可.
解答  解:以A为圆心,以AD长为半径画弧,交BC于G,连接AG,则AG=AD=3DE;作AF⊥BC,
解:以A为圆心,以AD长为半径画弧,交BC于G,连接AG,则AG=AD=3DE;作AF⊥BC,
∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,BF=FC,
∵BD=3,CE=4,
∴DF=FG=FE+1=$\frac{1}{2}$(DE+1).
∴AF2=AD2-DF2=(3DE)2-[$\frac{1}{2}$(DE+1)]2=9DE2-$\frac{1}{4}$(DE2+2DE+1)=$\frac{1}{4}$(35DE2-2DE-1),
∵BF=3+DF=3+$\frac{1}{2}$(DE+1)=$\frac{1}{2}$(DE+7),
∴BF2=$\frac{1}{4}$(DE2+14DE+49),
在等腰直角△ABC中,BF=CF,
∴BF=AF,
∴$\frac{1}{4}$(35DE2-2DE-1)=$\frac{1}{4}$(DE2+14DE+49),
整理得,17DE2-8DE-25=0
解得,DE=$\frac{25}{17}$或-1.(其中DE=-1舍去)
BC=BD+EC+DE=$\frac{144}{17}$,AF=BF=$\frac{1}{2}$BC=$\frac{72}{17}$.
△ABD的面积=$\frac{1}{2}$AFxBD=$\frac{1}{2}$×$\frac{72}{17}$×3=$\frac{108}{17}$.
点评 本题考查了等腰直角三角形的性质,勾股定理的应用,作出辅助线构建等腰三角形是解题的关键.

| A. | m<a<b<n | B. | a<m<n<b | C. | a<m<b<n | D. | m<a<n<b |
| A. | y=2x+3 | B. | y=2x-3 | C. | y=3x+2 | D. | y=3x-2 |

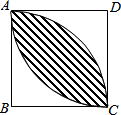 已知正方形ABCD的边长为a,分别以B,D为圆心,以a为半径画弧,如图所示,则阴影部分的面积为($\frac{1}{2}$π-1)a2.
已知正方形ABCD的边长为a,分别以B,D为圆心,以a为半径画弧,如图所示,则阴影部分的面积为($\frac{1}{2}$π-1)a2. 如图,在平面直角坐标系中,过点B(2,2)的直线AC,交y轴于点A(0,6),交x轴于点C.
如图,在平面直角坐标系中,过点B(2,2)的直线AC,交y轴于点A(0,6),交x轴于点C.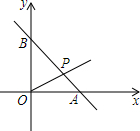 如图所示的直角坐标系中,O为坐标原点,直线y=-x+m与x轴、y轴交于A、B两点,且A的坐标为(4,0).
如图所示的直角坐标系中,O为坐标原点,直线y=-x+m与x轴、y轴交于A、B两点,且A的坐标为(4,0).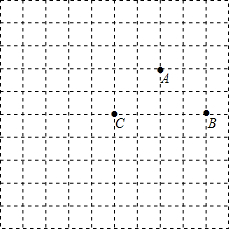 如图,网格中的每一个方格的边长都相等,点A,B,C都在网格的格点上,按要求完成下列各小题.
如图,网格中的每一个方格的边长都相等,点A,B,C都在网格的格点上,按要求完成下列各小题.