题目内容
6.已知a=$\sqrt{3}$+$\sqrt{2}$,b=$\sqrt{3}$-$\sqrt{2}$,求下列各式的值:(1)a2-b2;
(2)$\frac{1}{a}$+$\frac{1}{b}$;
(3)a2-ab+b2.
分析 先计算a+b、a-b、ab的值,然后把式子变形,再把a+b、a-b、ab的值代入化简后的式子计算即可.
解答 解:已知a=$\sqrt{3}$+$\sqrt{2}$,b=$\sqrt{3}$-$\sqrt{2}$,
a+b=2$\sqrt{3}$、a-b=2$\sqrt{2}$、ab=1,
(1)a2-b2)=(a+b)(a-b)=4$\sqrt{6}$
(2)$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$=2$\sqrt{3}$
(3)a2-ab+b2=(a+b)2-3ab=9
点评 本题考查的是二次根式的化简求值,把已知条件进行计算、把要求的代数式进行正确变形是解题的关键,注意因式分解在化简中的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,△DEF是由△ABC经过某种变换后得到的图形,分别写出点A与点D,点B与点E,点C与点F的坐标,你发现它们之间有怎样的关系?如果三角形ABC中任意一点M的坐标为(m,n),那么它在△DEF中对应点N的坐标是什么?
如图,△DEF是由△ABC经过某种变换后得到的图形,分别写出点A与点D,点B与点E,点C与点F的坐标,你发现它们之间有怎样的关系?如果三角形ABC中任意一点M的坐标为(m,n),那么它在△DEF中对应点N的坐标是什么? 如图,AB、CD交于点O,OE⊥AB,OF平分∠BOC,∠AOC:∠BOF=1:1,求∠DOE的度数.
如图,AB、CD交于点O,OE⊥AB,OF平分∠BOC,∠AOC:∠BOF=1:1,求∠DOE的度数.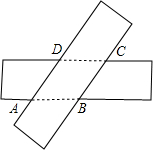 把两张宽度相等的矩形纸片叠放在一起,得到如图的四边形ABCD.
把两张宽度相等的矩形纸片叠放在一起,得到如图的四边形ABCD.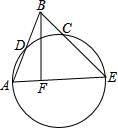 已知如图:D是⊙O劣弧AC的中点,连结AD并延长AD到B,使DB=AD,连结BC并延长交⊙O于E,连结AE,BF⊥AE于F.
已知如图:D是⊙O劣弧AC的中点,连结AD并延长AD到B,使DB=AD,连结BC并延长交⊙O于E,连结AE,BF⊥AE于F.