题目内容
18.如图1,两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.(1)在图1中,你发现线段AC、BD的数量关系是AC=BD;直线AC、BD的位置关系是AC⊥BD.
(2)将图1的△OAB绕点O顺时针旋转90°角,在图2中画出旋转后的△OAB.
(3)将图1中的△OAB绕点O顺时针旋转一个锐角,连接AC、BD得到图3,这时(1)中的两个结论是否成立?作出判断并说明理由.若△OAB绕点O继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
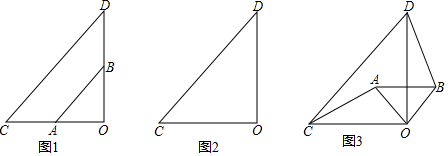
分析 (1)由△OAB和△OCD都是等腰直角三角形,即可判断出AC=DB,直线AC、BD相交成角的度数是90°;
(2)根据题意画出图形即可;
(3)由SAS证明△ACO≌△BOD,即可证明两个结论仍然成立.
解答 解:(1)∵△OAB和△OCD都是等腰直角三角形,且叠放在一起,
∴OA=OB,OC=OD,∠AOB=∠COD=90°,
∴AC=BD,AC⊥BD,
即线段AC、BD的数量关系是相等,直线AC、BD的位置关系是互相垂直;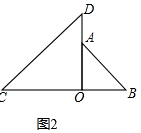
故答案为:AC=BD,AC⊥BD;
(2)如图2所示:
(3)将图1中的△OAB绕点O顺时针旋转一个锐角,(1)中的两个结论是否成立;理由如下:
∵旋转一个锐角后,∠COA+∠AOD=90°,∠BOD+∠AOD=90°,
∴∠COA=∠BOD,
在△COA和△DOB中,$\left\{\begin{array}{l}{OC=OD}&{\;}\\{∠COA=∠BOD}&{\;}\\{OA=OB}&{\;}\end{array}\right.$,
∴△COA≌△DOB(SAS),
∴AC=BD.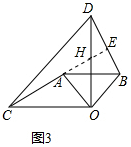
延长CA交OD于H,交BD于E,如图3所示:
∵△COA≌△DOB,
∴∠OCA=∠BDO,又∠DHE=∠CHO,
∴∠CED=∠COD=90°,
∴AC⊥BD;
将△OAB绕点O继续旋转更大的角时,结论仍然成立.理由同上.
点评 本题是三角形综合题目,考查了旋转的性质、等腰直角三角形的性质、全等三角形的判定与性质等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
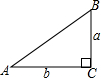 已知Rt△ABC中,两直角边长分别为a=2,b=3,斜边长为c.
已知Rt△ABC中,两直角边长分别为a=2,b=3,斜边长为c.