题目内容
在保护地球爱护家园活动中，校团委把一批树苗分给初三（1）班同学去栽种，如果每人分2棵，还剩42棵；如果前面每人分3棵，那么最后一人得到的树苗少于5棵，但至少分得一棵．
（1）设初三（1）班有x名同学，则这批树苗有 棵？（用含x的代数式表示）．
（2）如果前面每人分3棵，则最后一人得到的树苗有 棵？（用含x的代数式表示）
（3）初二（1）班至少有多少名同学？最多有多少名？
（1）设初三（1）班有x名同学，则这批树苗有
（2）如果前面每人分3棵，则最后一人得到的树苗有
（3）初二（1）班至少有多少名同学？最多有多少名？
考点：一元一次不等式组的应用
专题：
分析：（1）关键描述语是：每人分2棵，还剩42棵．树苗棵树=2×学生数+42；
（2）关键描述语：最后一人得到的树苗少于5棵；
（3）关键描述语是：最后一人得到的树苗少于5棵（但至少分得一棵）．则最后一人分得树苗数＞或等于1，＜5．
（2）关键描述语：最后一人得到的树苗少于5棵；
（3）关键描述语是：最后一人得到的树苗少于5棵（但至少分得一棵）．则最后一人分得树苗数＞或等于1，＜5．
解答：解：（1）这批树苗有（2x+42）棵；
（2）最后一人得到的树苗有2x+42-3（x-1）；
（2）根据题意，得
解这个不等式组，得40＜x≤44
答：初三（1）班至少有41名同学，最多有44名同学．
（2）最后一人得到的树苗有2x+42-3（x-1）；
（2）根据题意，得
|
解这个不等式组，得40＜x≤44
答：初三（1）班至少有41名同学，最多有44名同学．
点评：本题考查了一元一次不等式组的应用．解决问题的关键是读懂题意，找到关键描述语，找到所求的量的不等关系．
练习册系列答案
相关题目
记[a]为不大于a的最大整数，如[1.3]=1，[2]=2，[-2.3]=-3．不论对怎样的a，当x=[a]，y=[2a]时，关于x，y的已知多项式恒等于0．这个多项式可能是（ ）
| A、4x2+y2-4xy-2x+y |
| B、4x2+y2-4xy+2x-y |
| C、4x2+y2-4xy |
| D、4x2+y2-4xy+4x-2y+1 |
在函数y=
中，自变量x的取值范围是（ ）
| 1 | ||
|
| A、x＞-5 | B、x≥-5 |
| C、x＞0 | D、x≥0 |
若关于x的不等式（a+1）x＞2a+2的解集是x＜2，则a的取值范围为（ ）
| A、a＞0 | B、a＜0 |
| C、a＞-1 | D、a＜-1 |
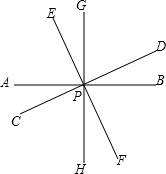如图，直线AB、CD、EF和GH相交于点P，且∠APC=25°，∠EPG=25°，∠BPF=65°，问哪些直线互相垂直？为什么？