题目内容
已知二次函数y=x2﹣(2k+1)x+k2+k(k>0)
(1)当k=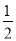 时,将这个二次函数的解析式写成顶点式;
时,将这个二次函数的解析式写成顶点式;
(2)求证:关于x的一元二次方程x2﹣(2k+1)x+k2+k=0有两个不相等的实数根.
(1)(1, )(2)证明见解析 【解析】试题分析:(1)把k代入抛物线解析式,然后利用配方法可确定抛物线的顶点坐标;(2)计算判别式的值,然后判别式的意义进行证明. 试题解析:(1)把k=代入y=x2﹣(2k+1)x+k2+k(k>0)得y=x2﹣2x+, 因为y=(x﹣1)2﹣ 所以抛物线的顶点坐标为(1,﹣ ); (2)△=(2k+1)2﹣4(k2+k)=1>0...
练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目


 B. 经过有交通信号灯的路口,遇到红灯
B. 经过有交通信号灯的路口,遇到红灯 中。
中。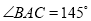 ,现将△
,现将△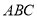 进行折叠,使顶点
进行折叠,使顶点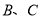 均与顶点
均与顶点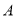 重合,则
重合,则 的度数为 .
的度数为 .
 的度数是( )
的度数是( ) 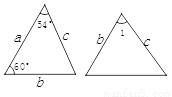
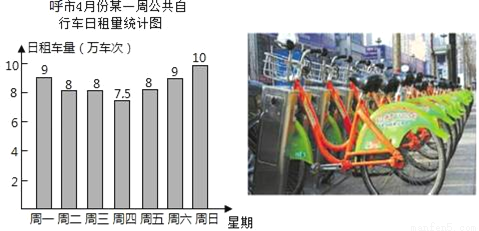
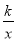 的一个交点A的坐标为(3,2),则它们的另一个交点B的坐标为_____.
的一个交点A的坐标为(3,2),则它们的另一个交点B的坐标为_____.
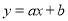 与
与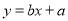 在同一直角坐标系中的图象位置可能是( ).
在同一直角坐标系中的图象位置可能是( ).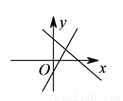 B.
B. 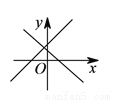
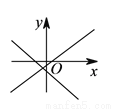 D.
D.